计组-数据的表示和运算

数据的检验

BCD 码

BCD 码用 4 位二进制数来表示 1 位十进制数中的 0~9 这 10 个数码，对于浮点数来说，BCD 码的最大作作用就是能和十进制完美对接，不会产生 精度损失 ，因为其他二进制编码表示浮点小数的时候，为离散的，像 0.3 这样的数浮点数就无法表示。但是 BCD 码因为四位表示十进制的一位，所以就没有这个问题。

奇偶校验码

奇校验码规定校验码的 1 有奇数个，也就是所有位（有效信息位+校验位）进行异或运算得到结果为 1

偶校验码规定校验码的 1 有偶数个，也就是所有位（有效信息位+校验位）进行异或运算得到结果为 0

这种校验码只能检测有奇数位发生错误的情况，不具备纠错能力。

海明码

海明码具有两位检错，一位纠错的能力。

首先设需要验证的位数为 n，需要 k 位作为校验位，根据公式：n+k<=2^k-1 计算出来所需要的额外验证位 k。

这些验证位在验证码的位置是按照二进制位权决定的，比如当 k 等于 3 的时候，在二进制里面就可以表示 1 2 4 这三个位权，那么就把所需要的 3 个验证位放在验证码的第 1 2 4 位上面。这是因为海明码的纠错是依靠判断验证位正确性然后将位权累加得到错误的地方，将验证位放到自己对应的位权的位置的话，一旦验证位错误也能获取错误的地方。这篇文章讲的很好：带你从头思考海明码的创造过程

验证位的计算也是根据分组决定的，分组的原因就是将某一个数据位的对错和几位位验证位绑定为一组，从而获取多组绑定结果。而分组的根据就是数据位在验证码的位权的二进制表示，比如一个数据位的位权是 5 也就是在验证码的地 5 位，那么 5 的二进制表示就是 101 对应分组就绑定到了 1 4 位上面的验证位上面了（想想为什么我们将验证位放到 2^n 上面），这样一旦 1 4 位的验证位验证失败，就可以一定确定是第 5 位出了错，因为只有第五位出错才会导致 1 4 位验证位同时验证失败。

这样我们就可以根据数据的二进制表示来分组了，分完组就可以计算验证位的值了，一般来说海明码这里采用偶验证，将某验证位加上他能表示的所有数据位一起进行偶验证得到 0，从而反计算得到此验证位的值。海明码验证的过程也是此过程，将所有的验证位按照上面的方式进行偶验证，结果正确表示 0，错误表示 1。

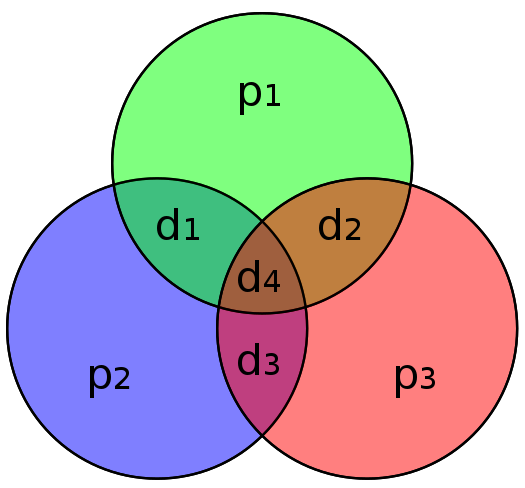
获取每一位验证位验证的结果之后，按照验证位位权将其求得十进制结果，得到错误数据位的标号。能得到原因就是因为分组，1 4 位验证位验证失败，一定是同时分到 1 4 位验证为组的数据位错误了，才能同时导致两个验证位失败，而同时分到 1 4 位的是第 4+1=5 位。

下面的图也可以参考验证位的分组。

数据的表示

定点小数和整数

定点数一般来说不怎么用到，虽然精度较高，但是表示的位数太低。

定点小数是一个纯小数，第一位为符号位，后面全都是小数点后面的位数，权值为 1-2^(-n)

定点整数是一个纯整数，第一位为符号位，后面全都是小数点前面的位数，权值为 2^n

移码

移码的作用主要是为了表示浮点数的阶码（也就是科学计数法乘上去的 2^n）。

那么作为根据它的用途，就需要满足以下特性：快速比对大小。（涉及到浮点数的计算必须比大小）

因此移码就是将 真值 向右偏移，使得负数变成正数。注意这里的移码是没有符号位的，通过加一个数将真值向右偏移，所有的数都是正数，可以快速比大小。

用 8bit 举例，经过偏移之后，00000000 表示原有的最小值 -2^8，11111111 表示原有的最大值 2^8-1。

位运算

对于位移运算来说，正数的原码、补码、反码、以及负数的原码，在进行位运算位移的时候，都是补零。

唯一的不一样的是，负数的补码，在向左移的时候添 0 效果等价于乘 2，向右移的时候补 1 效果等价于除 2 。这里可以想想补码原理相关。

定点数的乘法运算

定点数的原码乘法运算和我们手算乘法是一模一样的，不同的是，它全程只有占用三个寄存器，通用寄存器，ACC 寄存器，MQ 寄存器。其中通用寄存器和 MQ 寄存器初始存储乘数，而 ACC 寄存器最后和 MQ 寄存器一起存储乘积结果。运算原理如下图：

它通过检测 MQ 的最末尾值，如果为 1，那么在 ACC 中加上通用寄存器中的被乘数，为零则什么都不做，然后将 ACC 和 MQ 的内容一起左移一位。重复上面的步骤 MQ 的长度次数。最后 ACC 寄存器最后和 MQ 寄存器一起存储乘积结果。而符号位则直接采用两个乘数符号位的异或运算结果。

对于原码的乘法运算来说，还是很简单的，但是计算机里面的定点数为了方便减法的运算，一般都是用补码来存储，所以这里要么直接转化成原码，要么直接使用补码的乘法器。

---

这里的补码的乘法，有亿点点复杂，想了很久也没有想明白，只在知乎上找到了一个写的很好的文章，解释了 Booth 算法为什么要 Yn+1 - Yn 来决定是加还是减，用到了一点高中数列的知识。但是前面的很多推导他都省略了，结果导致根本看不懂。

下面是计算过程：

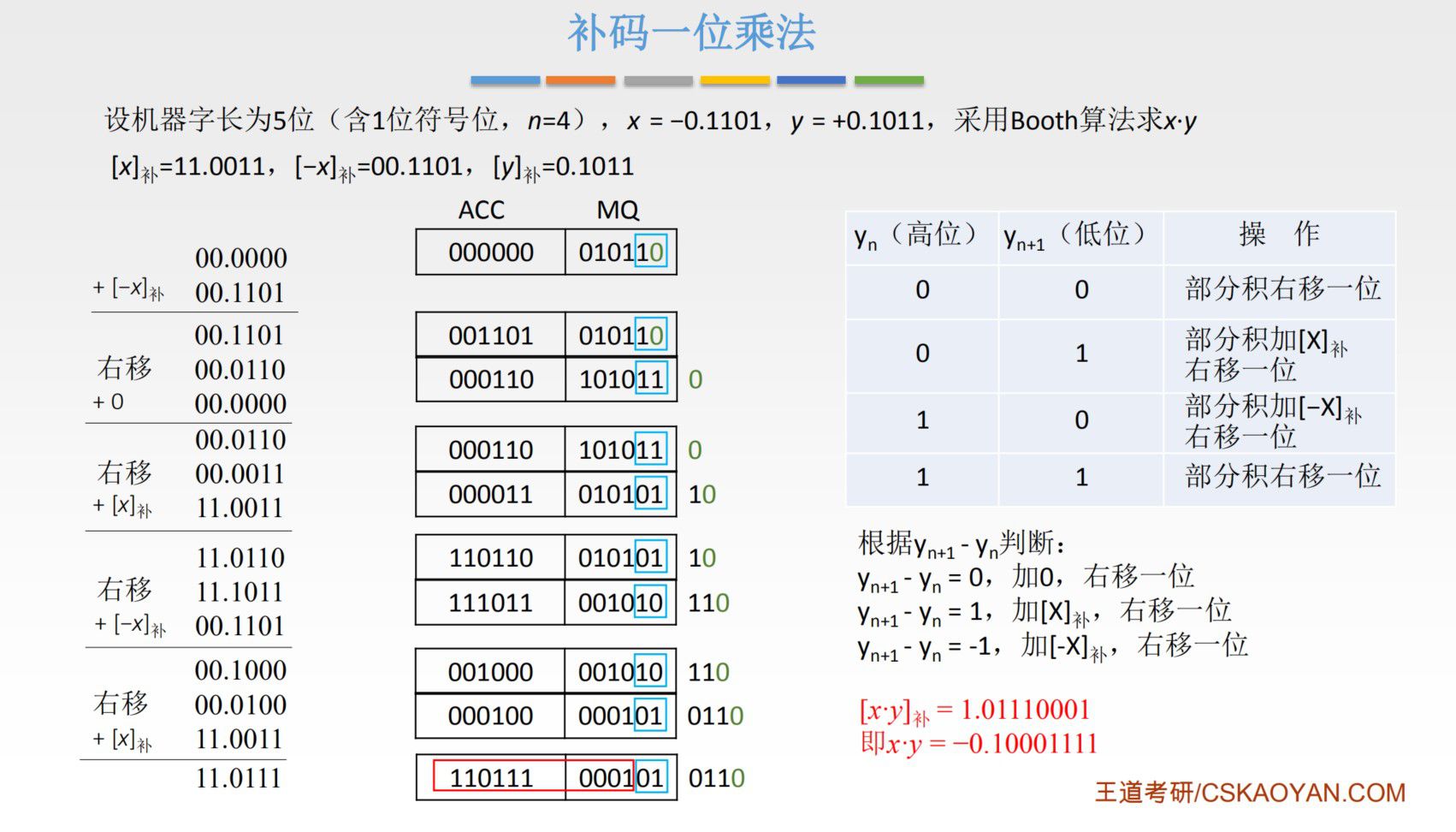
哭了，别说直观理解了，连推导过程都不给啊……

学个计组也太难了吧……

C 语言类型转化

里面的整形都使用的补码表示，long -> int -> short 都是直接截断后面的部分作为下一个类型的数据的，会直接丢失高位。

对于 double -> float 的尾数是丢失小数点最后几位的精度，而阶码则是截断后面部分舍去前面部分的。

IEEE 规范

浮点数在计算机中的表示方式为：

其中符号位 S 为一位，0 表示正，1 表示负，而指数位（阶码） E 使用移码来表示，偏移量为 2^n-1。数值位 M 使用原码，表示小数的尾数。

对于阶码，这里是根据补码进行加偏移量的，因为偏移量为 2^n-1 所以会导致表示范围为 -1 到 2*2^n -2，也就是说，阶码的实际表示范围为 1 到 2*2^n -2。

阶码 E 值	尾码 M 值	表示内容
0	0	浮点数为 0
0	≠0	表示为非规格化数尾数，没有默认的第一位 0.1
-1	0	表示为无穷大
-1	≠0	表示为 NaN，非数值

而尾数最终是需要被规格化的，规格化是指：将尾数部分化为 0.1XXXX 的形式，这样第一位的默认 1 就可以省略了。当然规格化的时候需要将阶码进行加减运算。

ALU 运算

对于加法的电路设计来说，因为需要获取上一位的进位信息，所以需要串行计算，总的延时有点高。那么为了降低延时，可以通过数学逻辑进行并行计算（某种意义上的真正的多线程），也就是每一位的获取的计算都是独立的。

首先构造一个并行的四位加法器，然后将四个四位加法器串行，得到一个较快的十六位加法器。（直接搞一个十六位并行的加法器电路设计过于复杂，所以还是四个拼接好了）

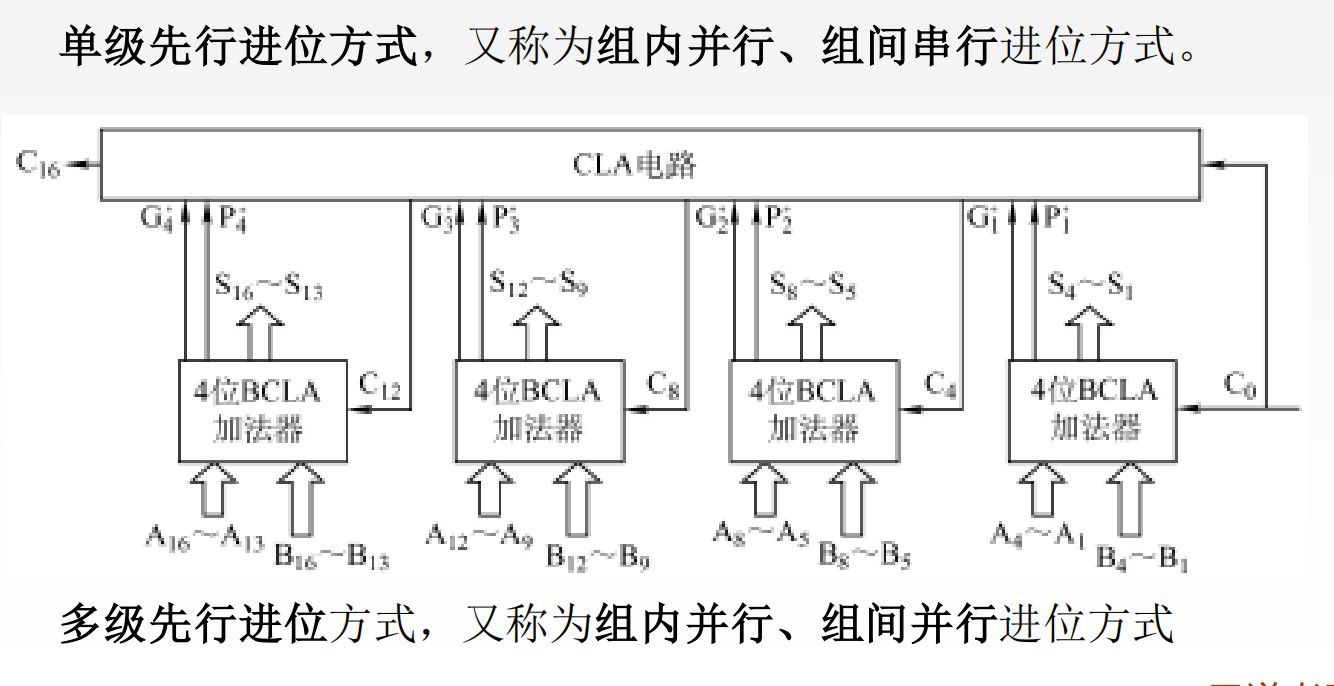
这里面的并行计算的数学推导有点复杂啊，不学了……