直接题目

P1283 HAOI2010 最长公共子序列

题目描述：

字符序列的子序列是指从给定字符序列中随意地（不一定连续）去掉若干个字符（可能一个也不去掉）后所形成的字符序列。令给定的字符序列X=“x0，x1，…，xm-1”，序列Y=“y0，y1，…，yk-1”是X的子序列，存在X的一个严格递增下标序列<i0，i1，…，ik-1>，使得对所有的j=0，1，…，k-1，有xij = yj。例如，X=“ABCBDAB”，Y=“BCDB”是X的一个子序列。 对给定的两个字符序列，求出他们最长的公共子序列。

输入：

两行序列，以”.”为结尾。

输出：

两行，最长公共子序列的长度和最长公共子序列的数量；

题解：

这道题的第一问是比较好求的，只需要列出状态转移方程：

1
2
3
f[i][j]=max(f[i][j],f[i-1][j-1]+1);
if(ch1[i]==ch2[j])
f[i][j]=max(f[i][j],f[i-1][j-1]+1);

但是关键在于第二问，第二问需要求出序列的数量，也就是所有的方案数，我们就可以建立一个数组 g[i][j] 表示在第一行字符i之前和第二行字符j之前，序列长度为 f[i][j] 的方案总数为 g[i][j] ，我们需要知道得出 f[i][j] 的方式。

当前如果 ch[i]==ch[j] 的时候，如果可以通过 f[i-1][j] （或者/和） f[i][j-1] 来原封不动的得到当前最优的 f[i][j] 那么 g[i-1][j] 和 g[i][j-1] 都能到达长度为 f[i][j] 的情况。并且因为 ch[i]==ch[j] 所以说通过 f[i-1][j-1]+1 得到的 f[i][j] 也一定是最优的。那么我么就可以列出这样的转移方程：

1
2
3
4
5
6
7
8
9
10
if(ch1[i]==ch2[j])
{

	int k1=0,k2=0,k3=0;
 	f[i][j]=max(f[i][j],f[i-1][j-1]+1);
	if(f[i][j]==f[i-1][j]) k1=1;
	if(f[i][j]==f[i][j-1]) k2=1;
	Get[i][j]=Get[i-1][j-1]+Get[i-1][j]*k1+Get[i][j-1]*k2;
	Get[i][j]%=100000000;
}

那么如果当前 ch[i]!=ch[j] 的时候呢我们需要判断 f[i-1][j-1] 是否等于f[i][j]，如果等于，就需要最后的 g[i][j] 中减去 g[i-1][j] 。因为一定有 f[i-1][j] 和 f[i][j-1] 更新了 f[i][j] ，并且 f[i-1][j] 和 f[j][i-1] 相等，这点可以根据 f[i-1][j-1]==f[i][j] 理解一下，所以说其实 g[i][j] 就是 g[i-1][j-1] 的值，但是我们加了两次，所以需要减掉。

1
2
3
4
5
6
7
8
9
else
{
	int k1=0,k2=0,k3=0;
	if(f[i][j]==f[i-1][j]) k1=1;
	if(f[i][j]==f[i][j-1]) k2=1;
	if(f[i][j]==f[i-1][j-1]) k3=1;
	Get[i][j]=Get[i-1][j]*k1+Get[i][j-1]*k2-Get[i-1][j-1]*k3;
	Get[i][j]%=100000000;
}

我们就可以解决这道题了，其实关键就是状态转移方程，当前最优值得出来的一个过程不好想到。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
char ch1[5100],ch2[5100];
int len1,len2;
int f[5100][5100];
int Get[5100][5100];
int main()
{
    memset(Get,0,sizeof(Get));
    memset(f,0,sizeof(f));
    char ch;
    cin>>ch;
    len1=0;
    while(ch!='.')
    {
        ch1[++len1]=ch;
        cin>>ch;
    }
    cin>>ch;
    len2=0;
    while(ch!='.')
    {
        ch2[++len2]=ch;
        cin>>ch;
    }
    for(int i=0;i<=len2;i++)
    {
        Get[0][i]=1;
        Get[i][0]=1;
    }
    for(int i=1;i<=len1;i++)
    for(int j=1;j<=len2;j++)
    {
        int k1=0,k2=0,k3=0;
        f[i][j]=max(f[i-1][j],f[i][j-1]);
        if(ch1[i]==ch2[j])
        {
            f[i][j]=max(f[i][j],f[i-1][j-1]+1);
            if(f[i][j]==f[i-1][j]) k1=1;
            if(f[i][j]==f[i][j-1]) k2=1;
            Get[i][j]=Get[i-1][j-1]+Get[i-1][j]*k1+Get[i][j-1]*k2;
            Get[i][j]%=100000000;
        }
        else
        {
            if(f[i][j]==f[i-1][j]) k1=1;
            if(f[i][j]==f[i][j-1]) k2=1;
            if(f[i][j]==f[i-1][j-1]) k3=1;
            Get[i][j]=Get[i-1][j]*k1+Get[i][j-1]*k2-Get[i-1][j-1]*k3;
            Get[i][j]%=100000000;
        }
    }
    cout<<f[len1][len2]<<endl;
    cout<<Get[len1][len2]<<endl;
    return 0;
}

P1284交错匹配

题目描述：

有两行自然数，UP[1..N] ，DOWN[1..M] ，如果 UP[I]=DOWN[J]=K ，那么上行的第I个位置的数就可以跟下行的第J个位置的数连一条线，称为一条K匹配，但是同一个位置的数最多只能连一条线。另外，每个K匹配都必须且至多跟一个L匹配相交且 K≠L 。现在要求一个最大的匹配数。 例如：以下两行数的最大匹配数为8.

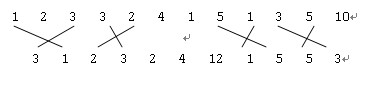
输入：

第一行有两个正整数N和M。第二行N个UP的自然数，第三行M个DOWN的自然数。其中0<N、M<=200，UP、DOWN的数都不超过32767。

输出：

最大匹配数；

题解：

首先感谢cdc的解题思路。

这道题也是比较魔性的，首先我们拿到这题是不是满脸蒙蔽，所以说我们需要想一下这道题的思路，我们列出状态设置f[i][j]表示在第一层第i个数和第二层第j个数的时候，交错匹配的最大值。然后我们首先用一个二重循环来找出在i和j之前的最大值，并赋值给f[i][j]。

然后我们就可以再次进行一个二重循环，枚举i和j之前，如果枚举到一个p和q能够将i和q，j和p进行一个二维交叉，美滋滋也就是说，在p和q的基础上，我们又多了一个方案，于是愉快的列出状态转移方程：

这道题和前面的也是一样的，状态转移方程是比较难想出来的，所以说我们要想方设法在前面找出继承给下一个最优值的方法，有时候题目上有很多乱七八糟的限制的时候，不停地结合数据范围，进行增加维度，然后想办法在新增加的维度里面尝试的解决这些乱七八糟的问题就可以了，动态规划还是需要进行多多联系，然后仔细想想方法。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include<cstring>
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m,a[201],b[201],f[201][201];
int main()
{
    memset(f,0,sizeof(f));
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    cin>>a[i];
    for(int i=1;i<=m;i++)
    cin>>b[i];
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        for(int k=1;k<=i;k++)
        for(int l=1;l<=j;l++)
        f[i][j]=max(f[i][j],f[k][l]);
        if(a[i]!=b[j])
        {
            for(int k=1;k<=i;k++)
            if(a[k]==b[j])
            for(int l=1;l<=j;l++)
            if(a[i]==b[l])
            f[i][j]=max(f[i][j],f[k-1][l-1]+1);
        }
    }
    cout<<f[n][m]*2<<endl;
    return 0;
}

P1296 传纸条 (NOIP2008 T3)

题目描述:

小渊♂和小轩♀是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个m行n列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标(1,1)，小轩坐在矩阵的右下角，坐标(m,n)。从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。 在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。 还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用0表示），可以用一个0-100的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度只和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入：

输入第一行有2个用空格隔开的整数m和n，表示班里有m行n列（1<=m,n<=50）。
接下来的m行是一个m*n的矩阵，矩阵中第i行j列的整数表示坐在第i行j列的学生的好心程度。每行的n个整数之间用空格隔开。

输出：

输出共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

题解：

NOIP的T3在我的印象里都是看不懂，不会做的题，没想到放到动态规划里面竟然如此简单（相对于其他T3来说），不过也是需要思考很久的，这里的状态设置方面是可以很容易想出来的，难的地方是“不难得出的状态转移方程”。

然后我们就开始愉快的解题过程了，这里建立一个 f[i][j][p][q] 一共四个状态，来表示传过来的纸条和回复的纸条在i,j和p,q的位置的时候，他们路过的好感度之和的最大值。

另外一个小优化，q可以通过i，j和p求出来，因为当前两个纸条经过的人数时相同的，那么我们可以用i+j-p来求出来q，这样可以省下来一重循环，然后我们就通过列出到达i,j和p,q的四种方案，也就是通过左和上转移过来的状态*2。然后我们就选择最大的加上新走到的位置 a[i][j] 和 a[p][q] 的值（如果两个纸条的位置相同那么就需要加上一个就好）。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<iostream>
#include<cstring>
#include<cstdio>
#include<iomanip>
#include<algorithm>
#include<cmath>
using namespace std;
int n,m,f[51][51][51][51];
int First,Second,q,a[100][100];
int main()
{
    memset(a,-1,sizeof(a));
    memset(f,0,sizeof(f));
    cin>>n>>m;
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    cin>>a[i][j];
    for(int i=1;i<=n;i++)
    for(int j=1;j<=m;j++)
    {
        for(int p=1;p<=n;p++)
        {
            if(i+j-p>0) q=i+j-p;//这里判断p能否计算出来
            else continue;//如果p不成立直接下一步
            f[i][j][p][q]=a[i][j]+a[p][q];
            First=max(f[i-1][j][p-1][q],f[i-1][j][p][q-1]);
            Second=max(f[i][j-1][p-1][q],f[i][j-1][p][q-1]);
            f[i][j][p][q]=max(First,Second)+a[i][j]+a[p][q];//四种组合的比较
            if(i==p&&j==q) f[i][j][p][q]-=a[i][j];//如果发现重复，要减去一遍
        }
    }
    cout<<f[n][m][n][m]<<endl;
    return 0;
}

后言：

下一个攻略的目标就是区间动态规划，加油！