考试总结
今天焦老师让我们写总结,我决定开始写总结,以前除了大型的考试意外都没有写过,以后怕不是要天天写了……
这次考试……emmmmmm 先看第一次测评的成绩:
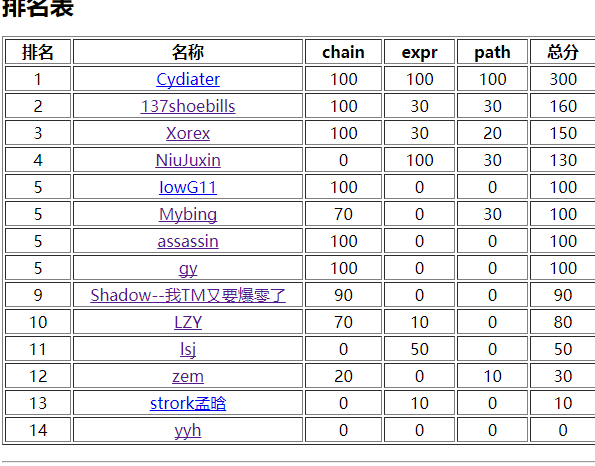
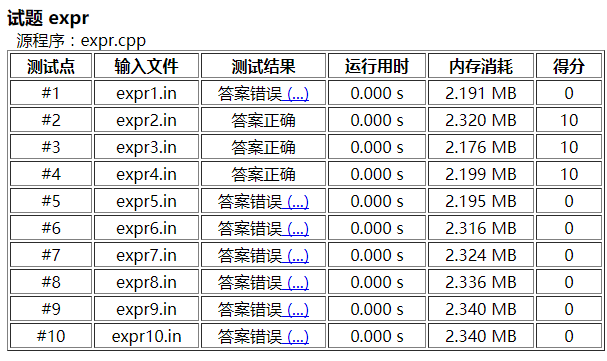
然后第一题谜之爆炸,第三题丢了一个点,还好还好没有炸的太狠……
这次考试过程是非常爽的,感觉节奏不错,首先先看第一题,然后花了一个半小时的时间写完了第一题,用的时间有些长了,其实应该控制在一个小时之内,但是这个第一题有些复杂……真的是不好写。以后尽量控制在一个小时以内。
写完第一题之后,开始看第二题,虽说是省选题,但是是比较简单的,问了帆神Map的使用方法,构建一个Topsort就能AC了,然后造了几个大数据,跑了跑没有问题。
写完前两题之后还剩下一个小时,看是看第三题,一眼秒暴力。想到原来黄山学长讲过怎么写,但是需要求组合数,虽然Century告诉了我组合数的公式,但是并不会求,就开始写暴力,复杂度O(n^2).二十分钟写完加调试。检查了一遍之后去吃饭了。
这次考试期望成绩是100+100+30,实际成绩是30+100+20。实力爆炸。
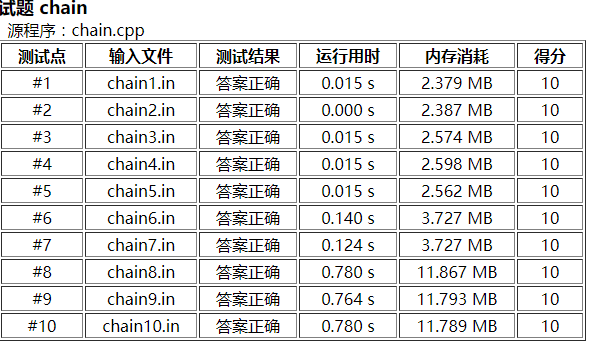
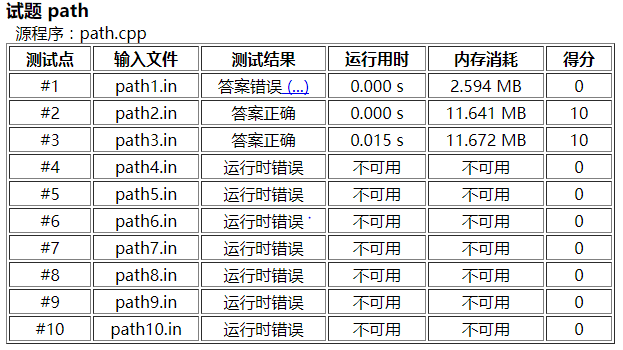
爆炸之后大家修改过后的成绩:
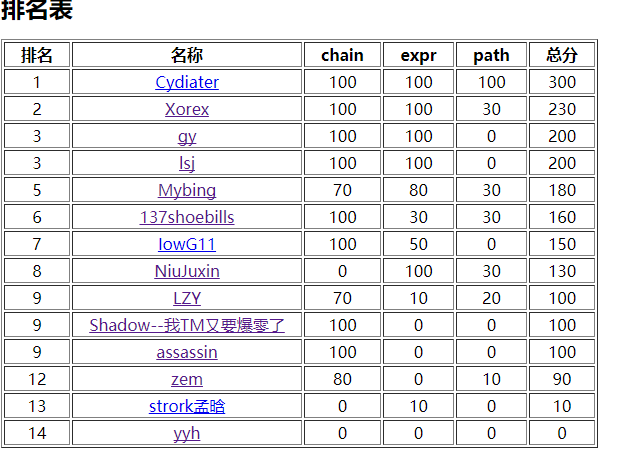
感觉以后写题的时候,需要注意两点,一点是把握好时间,T1尽量在一个小时内写完,而且要保证T1不会被炸掉。其次是暴力分数有可能不能拿全,要思考完整。
需要补充的知识点: 字符串哈希,乘法逆元;
勉为其难的写三篇题解吧……
表达式
题目描述
同学们需要先判 断给出的表达式是否合法。现在你的任务就是完成这个工作。
在本题中,我们对合法表达式定义如下:
- 任何连续(至少 1 个)数字是合法表达式;
- 若 x 是合法表达式,则(x)也是合法表达式;
- 若 x 和 y 是合法表达式,则 x+y、x-y、x*y、x/y 都是合法表达式;
- 若 x 是合法表达式,则在 x 前后添加任意数量的空白符也是合法表达式。 现在给你若干个表达式,请你判断这些表达式是否是合法的。
输入:
第 1 行为一个正整数 n,表示表达式个数; 接下来 n 行,每行一个字符串,表示给定的表达式。
输出:
共 n 行,若第 i 个表达式是合法的,就在第 i 行输出”Yes”(不含引号,下同),否则输出”No”。
题解:
题解没有什么好说的,就是使用while循环,然后每次寻找可以化为合法状态的字符串,把他们变成’1’,然后不停地合并为’1’,如果这次循环有改变字符串,那么久继续循环,如果没有改变,那么就结束循环。
判断最后的循环,如果里面只有两个元素,s1[0]=1和s1[1]=0; (这里字符串不知道为什么后面一定会有一个0),输出”Yes”即可,否则输出”No”;
需要注意的是把合法的化为’1’的过程的时候,有可能吧两个合法的区域化为一个,但其实他们是分开的,比如 “23333 66666” ,就会变成: 1 1 –> 1.那么只需要增加判断就行了,”()”也是同理。我就是这里炸掉的。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<string>
using namespace std;
int n,Len,Number,ID;
string s1,s2;
char a[2000];
bool Flag[200],Now;
void Work()
{
Number=false; Now=false;
for(int i=0;i<Len;i++)
{
if(isdigit(s1[i]))
{
while(isdigit(s1[i])) i++;
s2+='1';
}
s2+=s1[i];
}
s1=s2; s2.clear();
Len=s1.size();
while(!Now)
{
Now=true;
memset(Flag,false,sizeof(Flag));
for(int i=0;i<Len;i++)
{
if(s1[i]=='1')
{
Flag[i]=true;
if(s1[i+1]==')'&&s1[i-1]=='('&&s1[i+2]!='1'&&s1[i-2]!='1')
{
Flag[i-1]=true;
Flag[i+1]=true;
Now=false;
break;
}
if(s1[i-1]==' '&&s1[i-2]!='1')
{
ID=i-1;
Now=false;
while(s1[ID]==' ')
{
Flag[ID]=true;
ID--;
}
break;
}
if(s1[i+1]==' '&&s1[i+2]!='1')
{
ID=i+1;
Now=false;
while(s1[ID]==' ')
{
Flag[ID]=true;
ID++;
}
break;
}
if(s1[i+2]=='1')
{
if(s1[i+1]=='+')
{
Now=false;
Flag[i+1]=true;
Flag[i+2]=true;
break;
}
if(s1[i+1]=='-')
{
Now=false;
Flag[i+1]=true;
Flag[i+2]=true;
break;
}
if(s1[i+1]=='*')
{
Now=false;
Flag[i+1]=true;
Flag[i+2]=true;
break;
}
if(s1[i+1]=='/')
{
Now=false;
Flag[i+1]=true;
Flag[i+2]=true;
break;
}
}
}
}
for(int i=0;i<Len;i++)
{
if(Flag[i])
{
while(Flag[i]) i++;
s2+='1';
}
s2+=s1[i];
}
s1=s2; s2.clear();
Len=s1.size();
}
if(Len==2&&s1[0]=='1'&&s1[1]==0)
cout<<"Yes"<<endl;
else cout<<"No"<<endl;
}
int main()
{
freopen("expr.in","r",stdin);
freopen("expr.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
getchar();
scanf("%[^\n]",&a);
s1=a;
Len=s1.size();
Work();
}
return 0;
}
|
食物链
题目描述:
某研究小组经过长期的调查研究,在此地区发现了 n 个物种,并找到了它们之间 的m对捕食关系,由于物种众多,捕食关系复杂,他们希望你尽快地计算出食物链条数,以便下一步的研究工作。
输入:
第 1 行是正整数m,接下来m行有两个字符串A和B,分别代表对应的物种名称,描述了一对捕食关系A→B,表示A被B捕食(能量从A流动到B)。
输出:
仅一行,一个非负整数,为食物链条数对 1000000007 取模的值
题解:
这道题比较简单,我们需要使用Map或者字符串哈希来吧每一个字符串和一个数组一一映射,然后构建一个图。
然后进行拓扑排序,在拓扑排序的过程中,DP转移能量。
1
2
| for(int i=Link[x];i;i=a[i].Next)
F[a[i].Point]+=F[i];
|
然后如果这个点被加入队列并且这个点的初度为零,那么这个一定是F[i]条食物链的最顶端。我们让ans+=F[i]%Mod;就可以了。
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cctype>
#include<string>
#include<map>
using namespace std;
#define Mod 1000000007
struct Edge
{
int Next;
int Point;
}a[4000000];
map<string,int>::iterator it;
map<string,int>MapStr;
string s1;
int n,Number,len,Min,head,tail;
int First,Second,Link[200000];
long long F[200000],ans;
int Out[200000],Queue[200000];
int In[200000];
char c[20000];
void init(int x,int y)
{
a[++len].Point=y;
a[len].Next=Link[x];
Link[x]=len;
}
void TopSort()
{
for(int i=1;i<=Number;i++)
if(!Out[i])
{
F[i]=1;
Queue[++tail]=i;
}
Min=tail;
while(++head<=tail)
{
bool Flag=false;
int This=Queue[head];
for(int i=Link[This];i;i=a[i].Next)
{
Flag=true;
F[a[i].Point]+=F[This];
F[a[i].Point]%=Mod;
Out[a[i].Point]--;
if(!Out[a[i].Point])
Queue[++tail]=a[i].Point;
}
if(!Flag&&!In[This])
ans=(ans+F[This])%Mod;
}
cout<<ans%Mod<<endl;
}
int main()
{
freopen("chain.in","r",stdin);
freopen("chain.out","w",stdout);
cin>>n;
for(int i=1;i<=n;i++)
{
scanf("%s",&c); s1=c;
it=MapStr.find(s1);
if(it==MapStr.end())
{
MapStr[s1]=++Number;
First=Number;
}
else First=MapStr[s1];
scanf("%s",&c); s1=c;
it=MapStr.find(s1);
if(it==MapStr.end())
{
MapStr[s1]=++Number;
Second=Number;
}
else Second=MapStr[s1];
init(First,Second);
Out[Second]++;
In[First]++;
}
TopSort();
return 0;
}
|
路径
题目描述:
周三下午是模电实验课,xy 正打算从宿舍(0,0)去实验楼(n,m)上课,然而他突 然发现,由于暴雨的缘故,有 k 个路口(x,y)已经被水淹没(不知所措),根本过不了人。
xy 行走的路线很特别,必须满足:
- 一定平行于坐标轴;
- 只能在横纵坐标都 是整数的点改变方向;
- 行走过程中横坐标和纵坐标始终不减小。
现在有 xy 想知道有多少条满足条件的路线可以避开被淹没的路口到达实验
楼。
输入:
- 第1行是两个非负整数 n ,m,k表示实验楼的坐标和有 k 个路口被淹没。
- 接下来 k 行,每行有两个非负整数 x 和 y,表示(x, y)这个路口已被淹没
输出:
仅一行,一个非负整数,为满足条件的路线数对 1000000007 取模的值。
题解:
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
| #include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cctype>
using namespace std;
#define Mod 1000000007
int n,m,k,x,y;
long long F[2000][2000];
bool a[2000][2000];
inline int Read()
{
int F=true;
int This=false;
char ch=getchar();
while(!isdigit(ch))
{
if(ch=='-') F=-1;
ch=getchar();
}
while(isdigit(ch))
{
This=(This<<1)+(This<<3)+ch-'0';
ch=getchar();
}
return This*F;
}
int main()
{
freopen("path.in","r",stdin);
freopen("path.out","w",stdout);
n=Read(); m=Read(); k=Read();
for(int i=1;i<=k;i++)
{
x=Read();
y=Read();
a[x][y]=true;
}
for(int i=0;i<=n;i++)
for(int j=0;j<=m;j++)
{
if(a[i][j]) continue;
if(!i&&!j) F[i][j]=1;
if(i) F[i][j]+=F[i-1][j];
if(j) F[i][j]+=F[i][j-1];
F[i][j]%=Mod;
}
cout<<F[n][m]%Mod<<endl;
return 0;
}
|