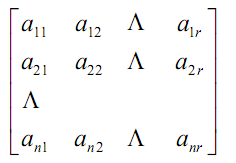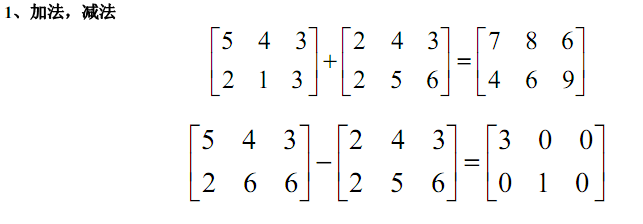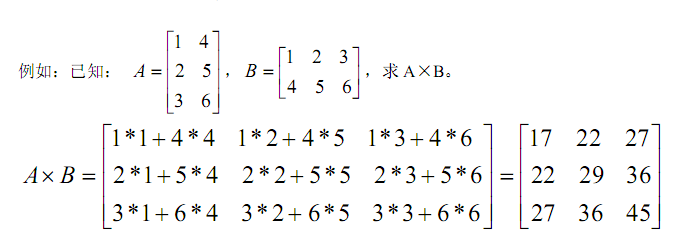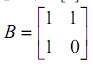快速幂
及其不要脸的Xorex终于要开始认真学习了QAQ,补一下前面漏下来的算法知识!
快速幂方法
顾名思义,快速幂就是快速算底数的n次幂。其时间复杂度为 O(log₂N), 与朴素的O(N)相比效率有了极大的提高,所以说这是一种二分的体现。
- 首先当我们计算一个数的次方的时候,比如2^10.那么我们按照常理的话,一定是这样计算的,
1
2
3
| long long ans=1;
for(int i=1;i<=10;i++)
ans=ans*2;
|
这样的话我们一共计算了10次。但是如果要求2^10000000000次幂的时候我们用地推就有可能超时了,那么我们可不可以优化一下呢。
将2^10转换为2^8*2^2的话,计算的次数就是最少的,也就是说,计算出来2^2需要1次,计算2^8需要计算2次,那么一共就需要计算4次就可以了。这样就大大增加了计算速度。
那么我们该如何拆分出来最简的计算呢,参照二进制,10的二进制就是1010,也就是10=2,1000=8,所以是2^2*2^8.
也就是说我们在计算的时候,只需要求出来指数的二进制形式,根据每一位上,如果存在1就计算这一位为1时表达出来的十进制的幂就好。
在转换为二进制每次进行计算的时候,相对应的幂也要进行计算也就是说当计算1010的时候,算到10,那么我们就要有一个变量的值为2^2,计算到010的时候,一个变量为2^3。这样在再结合二进制当前位是否是1,如果是,就将这个变量乘到ans上面modk就好。
代码模板
作为社会主义的好青年,我决定认真的把代码自己写出来!
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| #include<iostream>
using namespace std;
long long a,b,k,ans=true;
int main()
{
cin>>a>>b>>k;
cout<<a<<'^'<<b<<" mod "<<k<<'=';
while(b)
{
if(b%2) ans=ans*a%k;
b=(b>>true);
a=a*a%k;
}
cout<<ans<<endl;
return 0;
}
|
矩阵乘法
矩阵乘法其实就是一个矩阵相乘,矩阵的乘法最核心的用途就是在一些通过前面的一些数来地推出来后面的数的时候,可以通过矩阵相乘来表示地推的过程,然后将相同的矩阵相合并,就可以通过快速幂来解决问题。
首先矩阵的意思就是一个矩阵,如图:
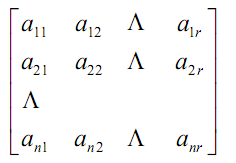
这就是一个矩阵,矩阵的加法和减法是很好理解的,直接相对应的每一位直接相加就好!如果两个矩阵的长和宽是不相等的,那么久没有办法进行相加减。
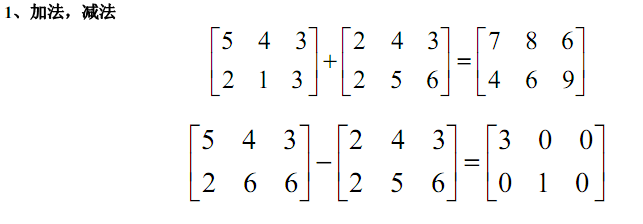
但是矩阵乘法就不一样了,矩阵乘法是一种非常神奇的东西,他的乘法和加减不一样,乘的时候矩阵的大小是第一个矩阵的高*第二个矩阵的宽。鬼知道为什么矩阵的运算方法为什么是这样的……所以说如果第一个矩阵的列数不等于第二个矩阵的行数,那么这两个矩阵是没有办法进行相乘的。
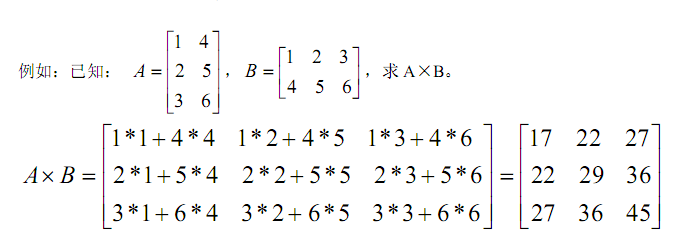
代码如下:
1
2
3
4
5
6
7
8
9
|
void Matrix_Mul(int n,int m,int p)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
for(int k=1;k<=p;k++)
c[i][j]+=a[i][k]*b[k][j];
}
|
代码很短,就像Floyd一样充满了美感。神奇的三重循环!
但是这个东西有什么用呢?矩阵乘起来效率真的是不能看啊!但是我们要祭出来神奇的菲波那切数列!
我们但知道,求菲波那切数列的复杂度是O(n)的,看起来并不高,但是如果要求1000000000000范围内的菲波那切数列呢。你是不是傻眼了……我们可以用矩阵乘法来优化一下。
首先,我们构造一个神奇的矩阵:
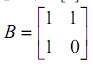
然后我们手里面有另外一个矩阵:A[F2,F1] ; 其中F1和F2表示的是数列的前两项。
然后我们让 A·B,得到的矩阵是什么?? [F3,F2],没错,如果是 A·B·B 呢?那么就是 [F4,F3],如果我们需要求出来第n项数列,我们只需要求 A·B·B·B…… (一共有n-2个B),也就是 A·B^(n-2) ,对于求出来 B^(n-2) 我们用快速幂直接开始求就好了,其复杂度为 logn 综合来看,总的复杂度是 (2r)3*logn 。
下面是及其不情愿才写出来的代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
| #include<iostream>
#include<cstring>
#include<cmath>
#include<algorithm>
#include<cstdio>
#include<cctype>
using namespace std;
long long a[10][10];
long long b[10][10];
long long c[10][10];
long long d[10][10];
long long number;
long long Mod=10000;
void Matrix_Two()
{
memset(c,false,sizeof(c));
for(long long i=1;i<=2;i++)
for(long long j=1;j<=2;j++)
for(long long k=1;k<=2;k++)
c[i][j]=(c[i][j]+b[i][k]*b[k][j])%Mod;
}
void Matrix_Ans()
{
memset(c,false,sizeof(c));
for(long long i=1;i<=2;i++)
for(long long j=1;j<=2;j++)
for(long long k=1;k<=2;k++)
c[i][j]=(c[i][j]+a[i][k]*b[k][j])%Mod;
}
void Matrix_Final()
{
memset(c,false,sizeof(c));
for(long long i=1;i<=1;i++)
for(long long j=1;j<=2;j++)
for(long long k=1;k<=2;k++)
c[i][j]=(c[i][j]+d[i][k]*a[k][j])%Mod;
}
void Matrix()
{
memset(a,false,sizeof(a));
memset(b,false,sizeof(b));
memset(c,false,sizeof(c));
memset(d,false,sizeof(d));
a[1][1]=1; a[1][2]=1;
a[2][1]=1; a[2][2]=0;
b[1][1]=1; b[1][2]=1;
b[2][1]=1; b[2][2]=0;
d[1][1]=1; d[1][2]=1;
}
bool Return()
{
if(number==0)
{
cout<<0<<endl;
return true;
}
if(number==1)
{
cout<<1<<endl;
return true;
}
if(number==2)
{
cout<<1<<endl;
return true;
}
if(number==3)
{
cout<<2<<endl;
return true;
}
return false;
}
void Matrix_Move_ans()
{
a[1][1]=c[1][1];
a[1][2]=c[1][2];
a[2][1]=c[2][1];
a[2][2]=c[2][2];
}
void Matrix_Move_Two()
{
b[1][1]=c[1][1];
b[1][2]=c[1][2];
b[2][1]=c[2][1];
b[2][2]=c[2][2];
}
void Fast_Fuck_PanYunTong(long long number)
{
while(number)
{
if(number&true)
{
Matrix_Ans();
Matrix_Move_ans();
}
number=(number>>true);
Matrix_Two();
Matrix_Move_Two();
}
Matrix_Final();
}
int main()
{
while(cin>>number)
{
Matrix();
if(Return()) continue;
if(number==-1) break;
Fast_Fuck_PanYunTong(number-3);
cout<<c[1][1]<<endl;
}
return 0;
}
|
不能再水了,马上就要到NOIP了,加油!
果然废柴就是这样,最近看到许多去雅礼中学参加培训的同学们都找到了目标。不停地奋斗着,而我已经成为了一枚咸鱼。LCY大神决心要面对HAOI和NOI,但是我这个咸鱼还在想着怎么在NOIP2017里面混一个一等奖。不管了,自己实力弱怨不得别人……