说在前面：

自从被刘老师赶出来机房了，没有办法好好在OJ上刷题，于是就借着各种闲杂课看看各种知识点吧，题目等到暑假的时候一定要刷个够。昨天老师基本没有讲什么课，所以就用来学习算法了。

Trie树

Trie树定义：

Trie,又称单词查找树,是一种树形结构，用于保存大量的字符串。它的优点是：利用字符串的公共前缀来节约存储空间。

Trie树构建：

Trie树拥有有3个基本性质：

  1. 根节点不包含字符，除根节点外每一个节点都只包含1个字符,每个节点都有26个分叉。
  2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。
  3. 每个节点的所有子节点包含的字符都不相同。

下面是个trie树的例子：

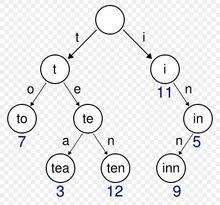
这里运用了非常巧妙的方法因为可能会出现各种字符重复，所以说这样就可以非常棒的进行存储，通过解决各种重复性的问题从而节约空间和查询的时间（效率是和字符串的重复度有关的）

在这个Trie结构中，保存了t、to、te、tea、ten、i、in、inn这8个字符串，仅占用8个字节

Trie树的每个节点下面应该有26[‘a’..’z’]个分支。当然，如果要区分大小写，就要多开了！一般都用指针来写，不过我们可以开个足够大的静态数组也可以。
基本26叉的数组，1万的容量基本是1M的存储空间。
按照竞赛的数据规模，我们用60万的静态数组完全足够了。

Trie树代码：

存储结构体

1
2
3
4
5
6
struct node
{
    char ch;
    int endflag;
    int Link[26];
}tree[610000];

Trie树的建立

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
void add(int k,int node)  //k是s的第k个字符，node为当前节点。
{
    int  chindex=s[k]-‘A’;  //字符的编号
    if (tree[node].link[chindex]==0)   //新开节点
	{
		tree[node].link[chindex]=++len;
		tree[len].ch=s[k];
		tree[len].endflag=false;
	}
	int nexnode=tree[node].link[chindex];  //下一个节点的下标
    if (k==(int)s.size()-1)
    {
        tree[nexnode].endflag=true;
        return;
    }
    add(k+1,nexnode);
}

Trie树的查询

1
2
3
4
5
6
7
8
9
10
11
bool find(int k, int last,int node)
//k是要查找字符串s的第k个元素
{
    int chindex=s[k]-'a';
    if (tree[node].link[chindex]==0)  return false;
    int nextnode=tree[node].link[chindex];
    if (k==(s.size()-1)) //如果k是最后一个字符
       if (tree[nextnode].endflag)  return true;
        else return false;
    return find(k+1,last,nextnode);
}

Aho-Corasick自动机

我们先来看一道题：

【P1366】给你N个单词(N <= 10000) ，再给一篇文章（文章长度len<=1000000 ）.
问有多少个单词在此文章中出现过。

【分析】基本的kmp 的时间复杂度是 N*len。KMP算法，它是用于单个串的线性匹配算法 .强大的p数组让KMP的匹配到了O(N)级别。
trie树在乎的是公共前缀。

那么，能不能在 trie树上做kmp呢？Kmp上的p数组很强大，我们肯定要在trie树上的每个节点构造出自己的p数组。一般的文章都是在trie树上开一个 fail域，有时候叫 fail指针，失败指针。

这就是AC自动机算法的核心思想。

AC自动机的原理：

Aho-Corasick自动机算法（简称AC自动机）1975年产生于贝尔实验室。该算法应用有限自动机巧妙地将字符比较转化为了状态转移。

AC自动机主要用于多关键字的字符串匹配。 要搞懂AC自动机，先得有模式树（字典树）Trie和KMP模式匹配算法的基础知识。

  • 如有模式串 { she, he, say, shr, her, ayd }
    要对串 yshersayd 进行匹配 。
    Kmp是对上面6个单词依次构造属于自己的P数组，依次枚举去验证。而AC自动机通过构造 失败指针 来 优化匹配，从而使算法复杂度达到 O(n)。

  • 失败指针是在所有模式串或其前缀中找一个最大的那个 K，即对于串 S1，我们在其它模式串或其前缀中找一个串 S2，使得S1[len(S1)- k, len(S1)]= S2[0, k] 其中 k 最大，则 S1[ len(S1) ] 的失败指针为 S2[ len(s2) ]。

  • 也可理解为当我们匹配失配时，利用已经匹配的结果，尽可能的将指针 i 往后移。

  • 如下图，当我们用 ‘shersayd’ 匹配时，匹配到 ‘e’ 时以后的字符失配，这时我们不是用 ‘hersayd’ 继续从头开始匹配。利用匹配的结果，我们可以只用 ‘sayd’ 在红圈的另外那个 ‘e’ 开始匹配。失败指针就是在匹配失败时转移，使得能够继续匹配。

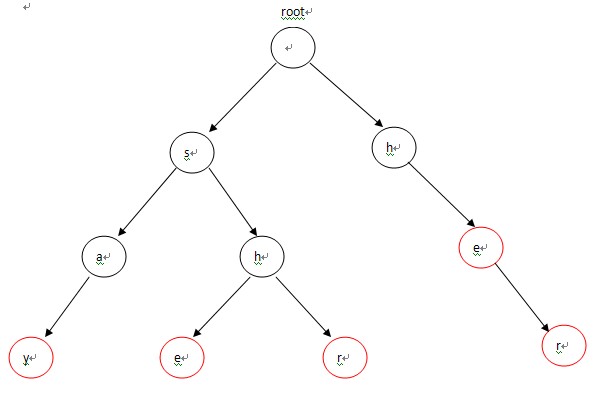
  • 上图中，粗红线表示失败指针，没标明失败指针的结点的失败指针都指向根结点。构建了失败指针后，匹配是如果不能匹配就从失败指针走，再匹配。如我们匹配刚才 那个字符串 ’yshersayd’，首先是字母 ‘y’ ，没有匹配，走向失败指针根结点，然后字母 ‘s’，匹配，走 向 ‘s’。然后字母 ‘h’，匹配，走向 ‘h’。然后字母 ‘e’ 走向 ‘e’，得到模式串 ‘she’。然后 ‘r’ ，这时 ‘r’ 失配，我们走向 ‘e’ 的失配指针，粗红线指向的另一个 ‘e’，继续匹配，得到模式串 ‘her’。依次进行。可知，匹配过程就是在一个图中走动，图中某一个结点标记了匹配了某个模式串。

AC自动机的实现：

AC自动机的实现有如下几步：

  1. 定义trie树结构
  2. 构造trie树
  3. 计算每个节点的fail指针。
  4. Fail指针的构造就是在trie树上不停的往回找。其原理就是用bfs得到trie的层次图，(下面这句话是重点) 当前节点的子节点的fail指针等于当前节点的fail指针的子节点。
  5. 进行查询

【细节】如果用c++的string。用cena评测发现大数据 c++的string的时间是 c语言 char 数组的4倍。
仔细体会下面的代码，然后自己一口气敲出来，就可以提交了。

AC自动机用一句话来定义就是在trie树上做kmp，fail域就是 kmp的p数组。这个是需要我们深刻理解的。

AC自动机的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
struct node
{
    int endflag; //是否是某个单词的最后一个字符.小心有多个重复的单词
    int fail;  //失败指针
    int link[26]; //26个分叉
} tree[510100];
char s[1001000];  //用字符数组代替字符串，在1000000 个字符条件下，速度会快一些。
//string s;
int n,m,len=0,ans,slen;
int head,tail,root=0;
int q[510000];
void add(int k,int node)  //k是s的第k个字符，root为当前节点。
{

    int chindex=s[k]-'a';
    if(tree[node].link[chindex]==0)   //新开节点
    {
        tree[node].link[chindex]=++len;
        tree[len].endflag=0; //因为存在有多个相同的单词
        tree[len].fail=root;
    }
    int nexnode=tree[node].link[chindex];
    if(k==slen-1)  //恰好是一个单词的结尾。
    {
        tree[nexnode].endflag++;
        return;
    }
    add(k+1,nexnode);
}
void init()
{
    scanf("%d\n",&n);
    memset(tree,0,sizeof(tree));
    for(int i=0;i<n;i++)
    {
        scanf("%s",s);
        slen=strlen(s);  //因为字符串比较多，用了c语言的字符串读入。
        add(0,root);
    }
}
void buildac()//生成fail指针，建好AC自动机
//用bfs生成一个层次序列，fail指针肯定往前跳。按层次依次求出fail指针
{
    head=tail=0;
    q[tail]=root;
    while (head<=tail) //bfs广度优先遍历 trie树
    {
        int now=q[head++];//  当前的节点
        int temp; //用来存储临时的fail指针，是tree的下标
        for(int i=0;i<26;i++)
        if(tree[now].link[i])  //求link[i].fail指针
        {
            int nextnode=tree[now].link[i];
            if(now!=root)//如果是根，那么fail肯定是root
            {
                temp=tree[now].fail;
                while(!tree[temp].link[i] && temp)//找不到与 link[i]匹配的前缀  且没有退到根
                temp=tree[temp].fail; //继续向上退
                tree[nextnode].fail=tree[temp].link[i];
            }
            q[++tail]=nextnode;  //让这个子节点进队。
        }
    }
}
void find()
{
    ans=0;
    int now=root;
    scanf("%s",s);
    len=strlen(s);  //这里用的也是c语言的字符。
    for(int i=0;i<len;i++)
    {
        int chindex=s[i]-'a';
        while( !tree[now].link[chindex] && now!=root)//如果找不到，往回返
        now=tree[now].fail;
        now=tree[now].link[chindex];//下一层传递。
        int temp=now;//如果找到某个单词
        while(temp!=root&& tree[temp].endflag>-1 ) //如果找到某个单词，累加到结果
        {
            ans+= tree[temp].endflag;
            tree[temp].endflag=-1;
            temp=tree[temp].fail;
        }
    }
    printf("%d",ans);
}
int main()
{
    init();
    buildac();
    find();
    return 0;
}