说在前面：

我要开字符串了，加油吧！↖(^ω^)↗

KMP算法

KMP算法用来解决的问题就是字符串匹配的问题（感觉和搜索引擎有些像），用来查找两个字符串中的子串归属的问题，感觉就像找关键字QAQ，不同于 O(N*M) 的暴力来说，KMP算法的复杂度为 O(n+m) 效率还是挺高的。

KMP算法的核心就是一个预处理，全靠一个叫Next的数组，他会告诉你在匹配失败的时候，应该回到那里进行再次匹配。这样可以节约很多的时间，但是实际感觉KMP的算法并不能快非常多，所以说字符串的处理是非常重要的，感觉光读入一个字符串所需要的时间都够 KMP 算法跑好几遍了……

具体原因请看《HAOI2017相同暴力算法为何差距如此之大》，一个80分一个10分，具体原因竟是C++的string的锅。

算法原理

我们在平常进行字符串查找的算法中，一般是直接进行枚举比对，但是如果当前比对错误，就直接在下一位从首位开始了，这无疑是浪费啊，如果我们能接着一段显然已经匹配好的进行匹配，无疑可以节约很多的时间。

而KMP算法之所以跑的飞快就是充分利用了目标字符串的性质（比如里面部分字符串的重复性，即使不存在重复字段，在比较时，实现最大的移动量）。

考察目标字符串ptr： ababaca

这里我们要计算一个长度为m的转移函数next。next数组的含义就是一个固定字符串的最长前缀和最长后缀相同的长度。比如：

  • abcjkdabc，那么这个数组的最长前缀和最长后缀相同必然是abc。

  • cbcbc 最长前缀和最长后缀相同是 cbc。

  • abcbc 最长前缀和最长后缀相同是不存在的。

注意最长前缀：是说以第一个字符开始，但是不包含最后一个字符。 比如aaaa相同的最长前缀和最长后缀是aaa。

  • 对于目标字符串ptr，ababaca，长度是7，所以next[0]，next[1]，next[2]，next[3]，next[4]，next[5]，next[6]分别计算的是a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀的长度。

  • 由于a，ab，aba，abab，ababa，ababac，ababaca的相同的最长前缀和最长后缀是“”，“”，“a”，“ab”，“aba”，“”，“a”,所以next数组的值是[-1,-1,0,1,2,-1,0]，这里-1表示不存在，0表示存在长度为1，2表示存在长度为3。这是为了和代码相对应。

比如：

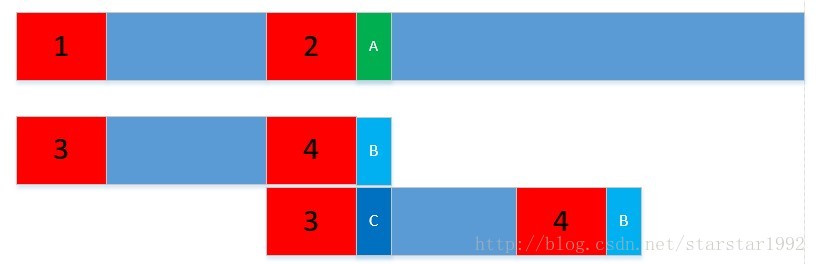
next数组就是说一旦在某处不匹配时（下图绿色位置A和B），移动ptr字符串，使str的对应的最大后缀（红色2）和ptr对应的最大前缀（红色3）对齐，然后比较A和Ｃ。

next数组的值，就是下次往前移动字符串ptr的移动距离。比如next中某个字符对应的值是4，则在该字符后的下一个字符不匹配时，可以直接移动往前移动ptr 5个长度，再次进行比较判别。

KMP的算法还是要好好的练习一下手速和理解啊。

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
void GetNext()
{
    int j=-1; Next[0]=-1;//因为字符串是从0开始，所以上一位为-1
    for(int i=1;i<b.size();i++)
    {//Next[i]表示的是对于字符串的i号字符的前缀，和开头的元素的最长匹配是多长
        while((j>=0)&&(b[j+1]!=b[i]))
        j=Next[j];//如果无法匹配，滚回到前面最长匹配的地方重新匹配
        if(b[j+1]==b[i]) j++;//如果匹配则前缀加一（j表示的是能匹配的最大长度）
        Next[i]=j;//确定最大匹配值也就是可以到的地方
    }
}
void KMP()
{
    int j=-1;//同样为-1
    for(int i=0;i<a.size();i++)
    {//这里a和b进行比较
        while((j>-1)&&(b[j+1]!=a[i])) j=Next[j];
        if(b[j+1]==a[i]) j++;
        if(j==b.size()-1)//b完全被匹配
        {
            j=Next[j];
            ans++;//这里来记录个数或位置等等；
        }
    }
}

例题

P1362字符串的自我匹配

题目描述：

给你一个字符串，它是由某个字符串不断自我连接形成的。但是这个字符串是不确定的，现在只想知道它的最短长度是多少.

输入：

第一行给出字符串的长度,1 < L ≤ 1,000,000. 第二行给出一个字符串，全由小写字母组成.

输出：

输出最短的长度

题解：

其实这道题就是一道结论题，考察你是否仔细理解了KMP算法的本质。

  • 我们首先要明白 Next[i] 这个数组表示的是什么，表示的对于你在b串比配到了第i个，发现卧槽不对了，但是你又不舍得b串从头开始在下一个a串字符上再次匹配，那么Next[i]存下来的就是b串中从头到Next[i]这些字符和a串上面所匹配的地方的前Next[i]是相同的，我们只需要从b串的Next[i]处开始和a串的下一个进行匹配就好了，因为前面的是一样的啊……

  • 所以说对于这道题，我们通过计算出来这个串的所有 Next[i] 这个数组的所有值，然后用这个串的长度n减去和自己的前缀相同的最大长度也就是Next[n]的值就好。

  • 为什么这样就可以呢，因为这个长长的字符串是若干个子串组成的，而子串都是完整的，那么Next[n]相同的前缀就是除掉最后一个子串以外所有的串的长度。总长度减去Next[n]就是最后一个子串的长度了。

算法真的是太神奇了QAQ

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cctype>
using namespace std;
int len,Next[1000001];
char ch[1000001];
int main()
{
    scanf("%d",&len);
    scanf("%s",&ch);
    int j=-1; Next[0]=-1;
    for(int i=1;i<len;i++)
    {
        while((j>-1)&&(ch[j+1]!=ch[i])) j=Next[j];
        if(ch[j+1]==ch[i]) j++;
        Next[i]=j;
    }
    cout<<len-Next[len-1]-1<<endl;
    return 0;
}