说在前面

  • 首先是最小割，这个最小割真的是非常Exciting啊，好像讲稿里面什么都没有些QAQ，真的是超级难受。然后自己百度了好久在弄明白了最小割的定义和求法（垃圾讲稿毁我青春！:angry:）

最小割

最小割定义：

割：设Ci为网络N中一些弧的集合，若从N中删去Ci中的所有弧能使得从源点Vs到汇点Vt的路集为空集时，称Ci为Vs和Vt间的一个割。通俗理解，一个图或网络的割，表示一个切面或切线，将图或网络分为分别包含源点和漏点的两个子集，该切线或切面与网络相交的楞或边的集合，称为图像的割。

最小割：最小割，图中所有的割中，边权值和最小的割为最小割

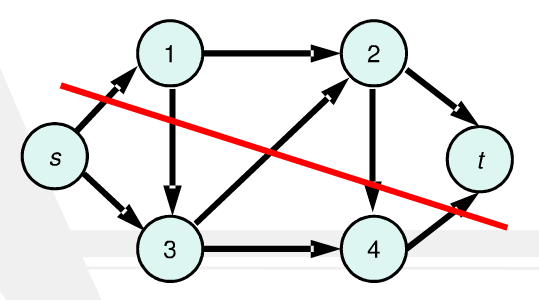
上面都是从百度百科里面粘过来的，用通俗易懂的话来说，假如你们家有一个复杂的水管路，然而你惹了 JZYZ 的 Centry 大佬，这位 Centry 大佬决定让你家没有水喝，一滴水都没有的那种，于是派Xorex 来执行任务。

Xorex 为了解决这个问题，只能用键盘砸断水管，这个砸断水管使得边不连通的过程就是割。但是有些水管粗有些细，粗的需要砸的时间长，细的则短一些，Xorex 也知道砸水管很耗费时间，那么这个设计最短时间断掉你家水源的方案就是一个最小割（最小割方案并不唯一）

比方说，水管公司是源点S，你家是汇点T，那么 Xorex 需要割掉一些代价和最小的边使得没有任何从S到T的通路，这样你家里就断水了哈哈哈哈……:smile:

最小割解法：

最小割的大小就是最大流的大小，我大概可以并不严谨的显然法来小小的证明一下：

  • 首先我们可以这样想，一个图的最大流是许多条路到汇点的流的大小，正是这些通路使得源点和汇点可以相连接，那么我们将这些通路打断就好了，那么该打断这些通路的哪一段呢？因为我们求得是最小割，所以自然就是流量最小的那一段了！然后我们将所有的边权最小的打断之后这样图一定是不连通的了。

  • 而求所有最短的边权可以利用求最大流来转化解决，在最大流的所有满流的边，都是这条通路的边权最小的边，因为如果存在更小的边权，那么上面的那条满流的边就不可能满流，流量而是边权最小的那个边的边权。

  • 这样最大流的大小就是漫流边边权之和，也就是最小割的大小了。

  • 那么如何来求出最小割的其中一种方案呢，我们在进行最大流计算完成之后，从原点进行遍历整张图，将遍历到的点标记为 true ；最终结束之后，所有标记为 true 的点和没有标记的点之间就是一个割边。

  • 那么为什么求出来的就是割边呢，因为最大流之后，所有通路在满流的那条通道处断掉了，也就是没有办法继续走下去，而这条通道一边标记为了 true 另一边没有被标记，那么他们之间就是一个割边了。

写出来真的是不容易呢QAQ

网络流 求法 建图
最大流 FF或Dinic 拆点，乱连
最小割 FF或Dinic 拆点，乱连

下面放上几道练习题吧，毕竟网络流这类题目最难得地方就是建图呢，超级不好建图，从最短路那里建立起来的自信心完全被 打爆 了……

P1320 Patrol

题目描述：

FJ有个农场，其中有n块土地，由m条边连起来。FJ的养牛场在土地1，在土地n有个新开张的雪糕店。Bessie经常偷偷溜到雪糕店，当Bessie去的时候，FJ就要跟上她。但是Bessie很聪明，她在从雪糕店返回时不会经过去雪糕店时经过的农场，因此FJ总是抓不住Bessie。
为了防止Bessie生病，FJ决定把一些诚实的狗放在一些土地(1和n除外)上，使Bessie无法在满足每块土地最多只经过一次的条件的情况下，从养牛场溜到雪糕店然后又溜回养牛场。
求出FJ最少要放多少只狗。数据保证1和n间没有直接的连边。

输入：

  1. 第一行：两个整数：n和m。
  2. 下面到M + 1：每行包含两个整数A和B是一条连接A和B的路径可以通过，沿着这两条路。没有踪迹会出现两次。

输出：

一个整数，需要放上狗的所有地方的数量。

题解：

这道题据说是网络流最小割的模板题，QAQ模板题都这么难，不愧是高级算法啊。

  • 首先还是建图，因为求最小割就是跑一遍Dinic的事，主要是能把整张图建立起来才行，这道题不同于割边的是，他是一个点隔断，那么我们可以将这个点进行拆开，拆成连个点，两个点之间连接一条权值为1的边，作为割边，也就是说，如果要割掉这个点，等价于割掉这个点和拆开的点之间的那条边，然后其他点点之间的连接权值就无所谓了，不过必须是大于零的，推荐使用1.

  • 这里需要注意的是，源点和汇点是不需要拆开的，不然等着徐王吧……还有建立点与点之间的连接的时候，除了拆点，源点，汇点为单向边以外，其他的两块地相连的为双向边。

  • 最后透露一个小坑，数据里面可能直接没有任何通路，也就是说你不需要放狗狗，那么就需要特判一下了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cmath>
#include<cctype>
using namespace std;
struct Edge
{
    int Point;
    int Next;
    int Value;
    int Back;
}a[80000];
int n,m,Level[8000],Link[8000],len;
int x,y,Maxx,Queue[8000],ans,all;
inline int In()
{
    int This=0,F=1; char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') F=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        This=This*10+ch-'0';
        ch=getchar();
    }
    return This*F;
}
void GetEdge_Frist(int x,int y,int z,int b,int c)
{
    a[++len].Point=y;
    a[len].Next=Link[x];
    a[len].Value=z;
    a[len].Back=len+1;
    Link[x]=len;
    a[++len].Point=c;
    a[len].Next=Link[b];
    a[len].Value=z;
    a[len].Back=len-1;
    Link[b]=len;
}
void GetEdge_Second(int x,int y,int z)
{
    a[++len].Point=y;
    a[len].Next=Link[x];
    a[len].Value=z;
    a[len].Back=len+1;
    Link[x]=len;
    a[++len].Point=x;
    a[len].Next=Link[y];
    a[len].Value=0;
    a[len].Back=len-1;
    Link[y]=len;
}
void GetEdge_Third(int x,int y,int z,int b,int c)
{
    a[++len].Point=y;
    a[len].Next=Link[x];
    a[len].Value=z;
    a[len].Back=len+1;
    Link[x]=len;
    a[++len].Point=c;
    a[len].Next=Link[b];
    a[len].Value=0;
    a[len].Back=len-1;
    Link[b]=len;
}
bool GetLevel()
{
    memset(Level,-1,sizeof(Level));
    int head=0,tail=1;
    Queue[1]=1; Level[1]=0;
    while(++head<=tail)
    for(int i=Link[Queue[head]];i;i=a[i].Next)
    if(Level[a[i].Point]<0&&a[i].Value)
    {
        Queue[++tail]=a[i].Point;
        Level[Queue[tail]]=Level[Queue[head]]+1;
    }
    return Level[Maxx]>=0;
}
int GetMaxFlow(int x,int Flow)
{
    if(x==Maxx) return Flow;
    int MaxFlow=0,d=0;
    for(int i=Link[x];i&&MaxFlow<Flow;i=a[i].Next)
    if(Level[a[i].Point]==Level[x]+1&&a[i].Value)
    if(d=GetMaxFlow(a[i].Point,min(a[i].Value,Flow-MaxFlow)))
    {
        MaxFlow+=d;
        a[i].Value-=d;
        a[a[i].Back].Value+=d;
    }
    if(!MaxFlow) Level[x]=-1;
    return MaxFlow;
}
void Dinic()
{
    while(GetLevel())
    while(ans=GetMaxFlow(1,123456789))
    all+=ans; return;
}
int main()
{
    n=In(); m=In();
    Maxx=n+n-2;
    for(int i=2;i<n;i++) //进行拆点
    GetEdge_Second(i,i+n-2,1);
    for(int i=1;i<=m;i++)
    {
        cin>>x>>y;
        if(x>y) swap(x,y);
        if(x==y) continue;//防止出现自环(Level可能可以自己解决)
        if(x!=1&&y!=1&&x!=n&&y!=n) GetEdge_Frist(x+n-2,y,1,y+n-2,x);
        else
        {
            if(x==1)
			{
				if(y==n) GetEdge_Third(x,y+n-2,1,y+n-2,x);
				else  GetEdge_Third(x,y,1,y+n-2,x);
				continue;
			}
			if(y==n)
			{
				if(x==1) GetEdge_Third(x,y+n-2,1,y+n-2,x);
				else GetEdge_Third(x+n-2,y+n-2,1,y+n-2,x);
                continue;
			}
        }
    }
    Dinic();
	if(!all) cout<<all<<endl;
	else cout<<all-1<<endl;
    return 0;
}

P1341被污染的牛奶

题目描述：

你第一天接手三鹿牛奶公司就发生了一件倒霉的事情：公司不小心发送了一批有三聚氰胺的牛奶。很不幸，你发现这件事的时候，有三聚氰胺的牛奶已经进入了送货网。这个送货网很大，而且关系复杂。你知道这批牛奶要发给哪个零售商，但是要把这批牛奶送到他手中有许多种途径。送货网由一些仓库和运输卡车组成，每辆卡车都在各自固定的两个仓库之间单向运输牛奶。在追查这些有三聚氰胺的牛奶的时候，有必要保证它不被送到零售商手里，所以必须使某些运输卡车停止运输，但是停止每辆卡车都会有一定的经济损失。你的任务是，在保证坏牛奶不送到零售商的前提下，制定出停止卡车运输的方案，使损失最小。

输入：

第一行: 两个整数N(2<=N<=32)、M(0<=M<=1000), N表示仓库的数目，M表示运输卡车的数量。仓库1代 表发货工厂，仓库N代表有三聚氰胺的牛奶要发往的零售商。 第2..M+1行: 每行3个整数Si,Ei,Ci。其中Si,Ei表示这 辆卡车的出发仓库，目的仓库。Ci(0 <= C i <= 2,000,000) 表示让这辆卡车停止运输的损失。

输出：

第1行两个整数c、t,c表示最小的损失，T表示要停止的最少卡车数。接下来t 行表示你要停止哪几条线路。如果有多种方案使损失最小，输出停止的线路最少的方案。如果仍然还有相同的方案，请选择开始输入顺序最小的。

题解：

我不会告诉你我整整写了一下午的QAQ

  • 首先这道题依然是非常魔性的（网络流的题目好像每一道都是很魔性的）这道题的第一问是非常简单的，也就是你需要跑一遍Dinic算法求出最大流就是题目中所要求的最小割，但是题目要求输出最小割的方案，而且对方案有一定的要求。

  • 也就是说，在输出方案的时候，你必须遵循一个原则就是割边的数量是最少的，并且先输入进去的边优先输出。那么这用常规的染色法显然是不行的。但是文档里面给的方法会超时的（可能是测评机老了），那么我们就可以用贪心来优化一下。

  • 我们需要另一个数组，记录下来输入边的坐标和权值，然后从大到小进行排序，那么排序，然后依次遍历，回流之后，将当前边的的权值设为零，然后跑一遍Dinic算法，看看最大流是否减少了当前边的权值，如果的确减少了这么多，那么这个边割掉就是符合题意的。

  • 首先回流的意思就是将权值分给反向弧的要回来，把图恢复成刚刚读入的状态。然后这种方法为什么正确就是因为，边的权值是从大到小排序的，所以说当前第一个选择割掉的话，是符合割边数量尽量小的，比如一条路上有两种满流，分别是一条权值为2的和两条权值为1的，那么我们割边就有两种方案了，要么割掉权值为2的，要么割掉两个权值为1的。那么我们经过排序之后，优先遍历到权值为2的，那么就割掉他了。

网络流的边与边之间的关系也是非常重要的。除非大量的做题，否则这种类型的题目考试真的难想出来QAQ

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<cctype>
using namespace std;
struct Edge
{
    int Point;
    int Back;
    int Value;
    int Next;
}a[20000];
struct GET_FIND
{
    int Value;
    int ID;
}b[20000];
int n,m,First,Second,Milk,Line,all_value;
int Link[2000],len,Queue[20000],sum;
int Level[2000],ans,all,ass[2000];
bool mycmp(GET_FIND First,GET_FIND Second)
{ return First.Value>Second.Value||(First.Value==Second.Value&&First.ID<Second.ID); }
inline int In()
{
    int This=0,F=1; char ch=getchar();
    while(!isdigit(ch))
    {
        if(ch=='-') F=-1;
        ch=getchar();
    }
    while(isdigit(ch))
    {
        This=This*10+ch-'0';
        ch=getchar();
    }
    return This*F;
}
void EdgeInit(int x,int y,int z,int w)
{
    a[++len].Point=y;
    a[len].Next=Link[x];
    a[len].Value=z;
    a[len].Back=len+1;
    Link[x]=len;
    a[++len].Point=x;
    a[len].Next=Link[y];
    a[len].Value=0;
    a[len].Back=len-1;
    Link[y]=len;
}
bool GetLevel()
{
    memset(Level,-1,sizeof(Level));
    int head=0,tail=1;
    Queue[1]=1; Level[1]=0;
    while(++head<=tail)
    for(int i=Link[Queue[head]];i;i=a[i].Next)
    if(Level[a[i].Point]<0&&a[i].Value)
    {
        Queue[++tail]=a[i].Point;
        Level[Queue[tail]]=Level[Queue[head]]+1;
    }
    return Level[n]>=0;
}
int GetMaxFlow(int x,int Flow)
{
    if(x==n) return Flow;
    int MaxFlow=0,d=0;
    for(int i=Link[x];i&&MaxFlow<Flow;i=a[i].Next)
    if(a[i].Value&&Level[a[i].Point]==Level[x]+1)
    if(d=GetMaxFlow(a[i].Point,min(a[i].Value,Flow-MaxFlow)))
    {
        MaxFlow+=d;
        a[i].Value-=d;
        a[a[i].Back].Value+=d;
    }
    if(!MaxFlow) Level[x]=-1;
    return MaxFlow;
}
void Dinic()
{
    while(GetLevel())
    while(ans=GetMaxFlow(1,123456789))
    all+=ans; return;
}
int main()
{
    n=In(); m=In();
    for(int i=1;i<=m;i++)
    {
        First=In(); Second=In(); Milk=In();
        EdgeInit(First,Second,Milk,i);
        b[i].ID=i; b[i].Value=Milk;
    }
    Dinic(); sum=all;
    cout<<all<<endl;
    for(int i=1;i<len;i+=2)
    {
        a[i].Value+=a[i+1].Value;
        a[i+1].Value=0;
    }
    sort(b+1,b+m+1,mycmp);
    for(int i=1;i<=m&&ans;i++)
    {
        int ID=b[i].ID;
        int Value=b[i].Value;
        ans=0;all=0;
        a[ID*2-1].Value=0;
        Dinic();
        for(int j=1;j<len;j+=2)
        {
            a[j].Value+=a[j+1].Value;
            a[j+1].Value=0;
        }
        if(sum-all==Value)
        {
            sum=all;
            ass[++Line]=ID;
        }
        else a[ID*2-1].Value=Value;
    }
    cout<<Line<<endl;
    sort(ass+1,ass+Line+1);
    for(int i=1;i<=Line;i++)
    cout<<ass[i]<<endl;
    return 0;
}