二叉搜索树(线段树)

线段树

线段树原理：

首先，线段树是一棵“树”，而且是一棵完全二叉树。同时，“线段”两字反映出线段树的另一个特点：每个节点表示的是一个“线段”，或者说是一个区间。事实上，一棵线段树的根节点表示的是“整体”的区间，而它的左右子树也是一棵线段树，分别表示的是这个区间的左半边和右半边。

线段树就是这样一种数据结构。它能够将我们需要处理的区间不相交的分成若干个小区间，每次维护都可以在这样一些分解后的区间上进行，并且查询的时候，我们也能够根据这些被分解了的区间上的信息合并出整个询问区间上的查询结构。

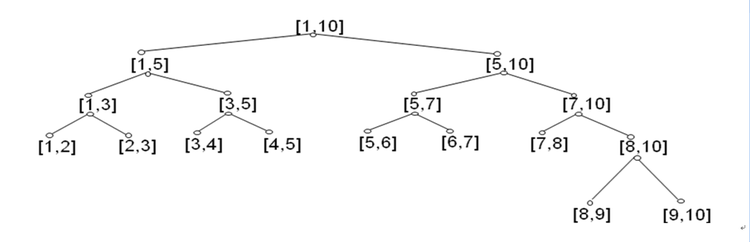
下面是个线段树（线段）的图示：

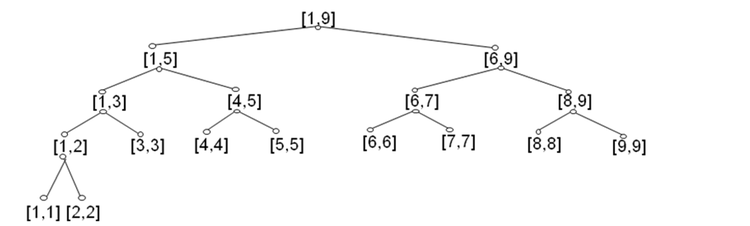
然后这个也是一个线段树（点）的图示：

我们就是利用这种方法搞的。

线段树模板(点)：

然后就是DFS模板：

查找最大值：

int Search(int Left,int Right,int Root)
{
    if(y<Left||x>Right) return -123456789;
    if(x<=Left&&y>=Right) return a[Root];
    int Mid=(Left+Right)/2;
    int First=Search(Left,Mid,Root*2);
    int Second=Search(Mid+1,Right,Root*2+1);
    return max(First,Second);
}

修改值：

void Change(int Left,int Right,int Root)
{
    if(x<Left||x>Right) return;
    if(Left==Right)
    {
        a[Root]=y;
        return;
    }
    int Mid=(Left+Right)/2;
    Change(Left,Mid,Root*2);
    Change(Mid+1,Right,Root*2+1);
    a[Root]=max(a[Root*2],a[Root*2+1]);
}

但是这个仅仅只是一个模板而已。

如果我们需要一种修改一个区间的东西，那么我们上面的方法就不可以了，比如下面的一道题，需要修改一个区间的值。

P1244线段树例题b

题目描述：

给定一个包含n个数的序列，初值全为0，现对这个序列有两种操作：

操作1：把 给定 第k1 个数改为k2;

操作2：查询 从第k1个数到第k2个数得最大值。（k1<=k2<=n）
所有的数都 <=100000

输入：

第一行给定一个整数n，表示有n个操作。 以下接着n行，每行三个整数，表示一个操作

输出：

若干行，查询一次，输出一次。

题解：

这道题刚刚开始我使用的方法就是上去一个离散化，用一个数组记录下来对于一个区间的 Lazy 标记（伪），然后在计算最大值的时候加上去这个标记。然后就去了 Debug 发现了一个非常严重的问题这里的n不是一共有n个数，而是下面有n个操作，所以说枚举的范围需要自己找到最大值进行计算。

然后修改之后，发现还是不对，然后自己就开始一步一步的进行打表跟踪，发现自己的离散化在遇到一些特别的情况之下会没有办法处理（梦想破裂乖乖去看了题解），然后题解上面是用到了标记下传的方法，更新 Lazy 之后，利用 DFS 将 Lazy 标记进行下传，然后这样就可以修改了最基础的值，不过要记得下传了 Lazy 标记之后要进行清零。同时下传的时候顺便更新一遍最大值。

这里利用的就是如果需要查找到这个值的话，一路上的 Lazy 和最优值都会进行顺便更新，确保最后的一定就是最优值，然后这样需要的时候进行标记下传，不需要的时候就将其保留下来，留到最后需要使用的时候。有些类似于离散化，这样会可以大大的减少不必要的更新。

代码：

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;
struct Edge
{
    int ID;
    int X;
    int Y;
}IN[400000];
int n,a[400000],x,y,z,Lazy[400000],maxx;
inline int Read()
{
    int This=0; char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9')
    { This=This*10+ch-'0'; ch=getchar(); }
    return This;
}
int Search(int Left,int Right,int Root)
{
    if(y<Left||x>Right) return -123456789;
    if(Left>=x&&Right<=y) return a[Root];
    a[Root*2]+=Lazy[Root];
    a[Root*2+1]+=Lazy[Root];
    Lazy[Root*2]+=Lazy[Root];
    Lazy[Root*2+1]+=Lazy[Root];
    Lazy[Root]=0;
    int Mid=(Left+Right)/2;
    int First=Search(Left,Mid,Root*2);
    int Second=Search(Mid+1,Right,Root*2+1);
    return max(First,Second);
}
void Change(int Left,int Right,int Root)
{
    if(Left>y||Right<x) return;
    if(Left>=x&&Right<=y)
    {
        Lazy[Root]++;
        a[Root]++;
        return;
    }
    a[Root*2]+=Lazy[Root];
    a[Root*2+1]+=Lazy[Root];
    Lazy[Root*2]+=Lazy[Root];
    Lazy[Root*2+1]+=Lazy[Root];
    Lazy[Root]=0;
    int Mid=(Left+Right)/2;
    Change(Left,Mid,Root*2);
    Change(Mid+1,Right,Root*2+1);
    a[Root]=max(a[Root*2],a[Root*2+1]);
}
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        IN[i].ID=Read();
        IN[i].X=Read();
        IN[i].Y=Read();
        maxx=max(maxx,IN[i].Y);
    }
    for(int i=1;i<=n;i++)
    {
        x=IN[i].X; y=IN[i].Y; z=IN[i].ID;
        if(z==1) Change(1,maxx,1);
        if(z==2) cout<<Search(1,maxx,1)<<endl;
    }
    return 0;
}

P1247贪婪大陆

题目描述：

人类被蚂蚁们逼到了 Greed Island 上的一个海湾。现在，小 孟晗 的后方是一望无际的大海， 前方是变异了的超 级蚂蚁。 小 孟晗 还有大好前程，他可不想命丧于此， 于是他派遣手下最后一批改造 SCV 布置地雷以阻挡蚂蚁们的进攻。 小 孟晗 最后一道防线是一条长度为 N 的战壕， 小 孟晗 拥有无数多种地雷，而 SCV 每次 可以在[ L , R ]区间埋放同一种不同于之前已经埋放的地雷。 由于情况已经十万火急，小 孟晗 在某些时候可能会询问你在[ L’ , R’] 区间内有多少种不同的地雷， 他希望你能尽快的给 予答复。

输入：

第一行为两个整数 n 和 m； n 表示防线长度， m 表示 SCV 布雷次数及小 孟晗 询问 的次数总和。 接下来有 m 行， 每行三个整数 Q，L , R； 若 Q=1 则表示 SCV 在[ L , R ]这段区间 布上一种地雷， 若 Q=2 则表示小 孟晗 询问当前[ L , R ]区间总共有多少种地雷。

输出：

对于小 孟晗 的每次询问，输出一个答案（单独一行），表示当前区间地雷总数。

题解：

这道题，怎么说呢，超级恶心超级恶心！！！

不过学到了一招，正难则反，还有另一个在上一题学到的线段覆盖贪心定理。

刚刚开始的时候，我的策略就是如果一个区间里面和要放地雷的区间有交集，那么就让他们的数量+1，然后发现在搜索最大值的时候有些区间是分开的，也就是说没有办法一下子得到最大值，需要进行分区间，而分开的区间没有办法得出真正的地雷数，以为无论是取最大值还是求和都没有办法计算出来地雷数量。

然后我看到了题解里面的一句话，正难则反，百度了之后才明白，若果正着不好求出来这个值的时候，那么就可以尝试进行倒推，反着进行计算。

既然我们需要求出来这个区间里面的，和区间相交的线段的条数之和（将布置上一排地雷视为一个线段），那么我们只要求出有多少个线段没有和当前查询区间相交就可以了，如果没有和当前区间相交，那么我们就可以在区间左边找到线段右端的数量，在区间右边找到线段左端的数量，两个之和就是没有和区间相交的数量，这样就求出来了最终答案。

还有一个线段覆盖贪心定理，策略就是将线段右端点进行升序排序，如果右端点相同则左端点降序排序，然后排在前面的优先度高（似乎是通用类型）

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int n,m,x,y,z,Num_Right[400000];
int ans,all,Num_Left[400000];
inline int In()
{
    int This=0;char ch=getchar();
    while(ch<'0'||ch>'9') ch=getchar();
    while(ch>='0'&&ch<='9')
    {This=This*10+ch-'0';ch=getchar();}
    return This;
}
void Change(int Left,int Right,int Root)
{
    if(Left>y||Right<x) return;
    if(Left>x&&Right<y) return;
    if((Left==x&&Right==x)||(Left==y&&Right==y))
    {
        if(Left==x&&Right==x)
        Num_Left[Root]++;
        if(Left==y&&Right==y)
        Num_Right[Root]++;
        return;
    }
    int Mid=(Left+Right)/2;
    Change(Left,Mid,Root*2);
    Change(Mid+1,Right,Root*2+1);
    Num_Left[Root]=Num_Left[Root*2]+Num_Left[Root*2+1];
    Num_Right[Root]=Num_Right[Root*2]+Num_Right[Root*2+1];
}
int Search_Right(int Left,int Right,int Root)
{
    if(Left>y||Right<x) return 0;
    if(Left>=x&&Right<=y) return Num_Left[Root];
    int Mid=(Left+Right)/2;
    int First=Search_Right(Left,Mid,Root*2);
    int Second=Search_Right(Mid+1,Right,Root*2+1);
    return First+Second;
}
int Search_Left(int Left,int Right,int Root)
{
    if(Left>y||Right<x) return 0;
    if(Left>=x&&Right<=y) return Num_Right[Root];
    int Mid=(Left+Right)/2;
    int First=Search_Left(Left,Mid,Root*2);
    int Second=Search_Left(Mid+1,Right,Root*2+1);
    return First+Second;
}
int main()
{
    n=In(); m=In();
    for(int i=1;i<=m;i++)
    {
        z=In(); x=In(); y=In();
        if(z==1)
        { Change(1,n,1); all++; }
        if(z==2)
        {
            int First=x,Second=y;
            x=1;y=First-1;
            ans=Search_Left(1,n,1);
            x=Second+1;y=n;
            ans+=Search_Right(1,n,1);
            cout<<all-ans<<endl;
        }
    }
    return 0;
}