说在前面

今天写的这道题怕是我目前见过最神奇的东西，比当初见到Floyd还要神奇的东西，这个斜率优化啊，和DP里面一些普通的斜率优化简直强到了离谱好吧，我来总结一下。

P1660最佳牛栏

题目描述：

农场主 John (简称 FJ) 的农场有一长排的 N (1 <= N <= 100,000)块地组成. 每块地有一定数量 (ncows) 的牛, 1 <= ncows <=2000. FJ 想修建环绕邻接的一组地块的栅栏, 以最大化这组地块中平均每块地中牛的个数. 这组地块必须包含至少 F (1 <= F <= N) 块地, F 作为输入给出. 给定约束, 计算出栅栏的布置情况以最大化平均数.

输入：

  1. 行 1: 空格分隔的两个整数, N 和 F.
  2. 行 2..N+1: 每行包含一个整数, 一块地中的牛数.
  3. 行 2 给出地块 1 中的牛数,
  4. 行 3 给出地块 2 中的牛数.

输出：

行 1: 一个整数, 它是最大平均数的 1000 倍. 不要用舍入求整, 仅仅输出整数 1000*ncows/nfields.

题解：

这道题不是一道DP，没有状态转移方程，只需要记录一个最优值就好了，这道题暴力非常爽，二重循环能拿72分，一重循环钦定长度为最小能拿52分，也就是这种题考试的时候一定要敲暴力，就算知道正解看到能水到不错的分数就敲吧，毕竟正解是有坑的，比如n=f和斜率相同，翻车爆零很有可能，相同情况请参看我 NOIP Day2T1 爆零记。

贪心害死人！

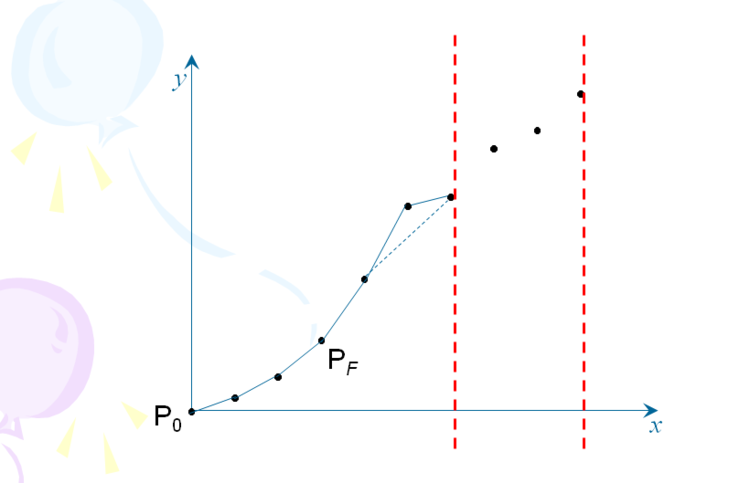
这道题的优化策略就在于在寻找结尾为i的序列最大值的时候，可以通过斜率来找最优值。首先计算出来牛的数量前缀和a[i]，然后可以轻易的得出，对于集合i到j中，其斜率也就是平均值就是 (a[i]-a[j])/(i-j) ，那么我们如何 O(1) 的时间里面求出最优值呢，我们可以画出来一个图，其中和坐标表示的就是i，纵坐标表示 a[i] ，由于 a[i] 为前缀和，所以可以保证当 i>j 的时候 a[i]>a[j] 。

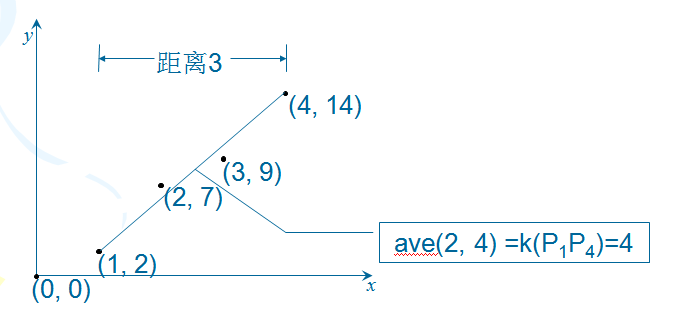
然后两个点之间的连线的那条线的斜率其实就是平均值！所以我们就可以转换到几何的角度上去解决问题了。

那么我们如何找出一个点要比另外一个点优秀呢，也就是说我们在用队列维护的时候，如何淘汰掉不优的点呢。

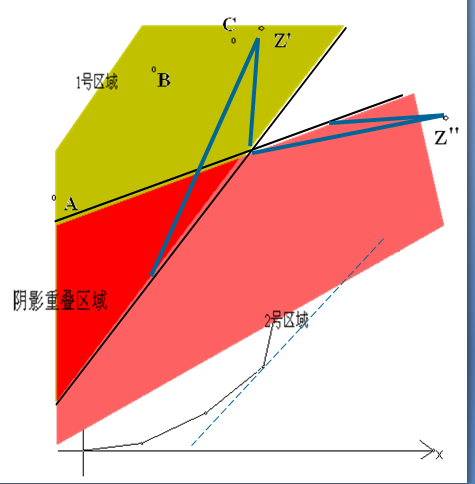
看到上面的图片，我们就可以得出，

–若k(BZ)大于k(AZ) ?Z在1号区域

–若k(BZ)大于k(CZ) ?Z在2号区域

–若k(BZ)最大 Z在阴影重叠区域

但是我们已经证明过了了，z这个点一定是在b的右边的时候，所以说BZ最大是不成立的，那么我们就可以将BZ删除掉了

具体的维护过程如下：

这个时候我们进行更新队列

震惊！突然发现斜率不是单调递增的了！

直接维护掉了，这个点反正不会是最优值了。

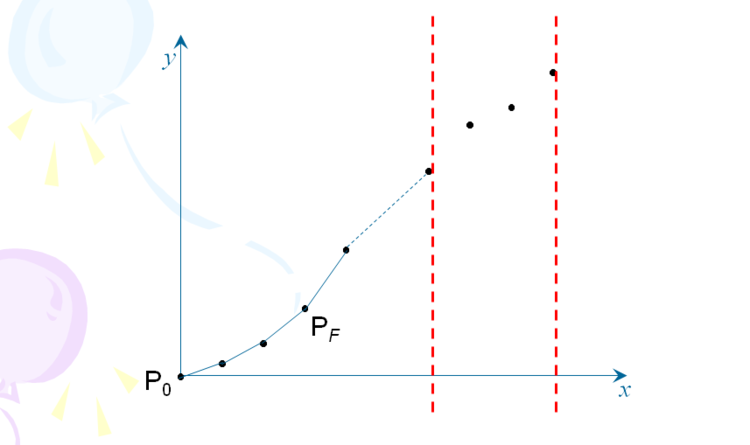
好的我们清楚掉了队列中的不会是最优的值。

之后我们就这样不断的循环下去，加入一个新的点，然后开始更新（注意用while）

这样我们就得到了一个斜率为递增的一个队列，那么我们该如何寻找最优的斜率呢，如果枚举的话，恐怕有可能超时的，不过这个队列是单调的，我们就可以用单调性来进行优化。

也就是说我们找的最优值从j到i其实就是j连接i为最大斜率。

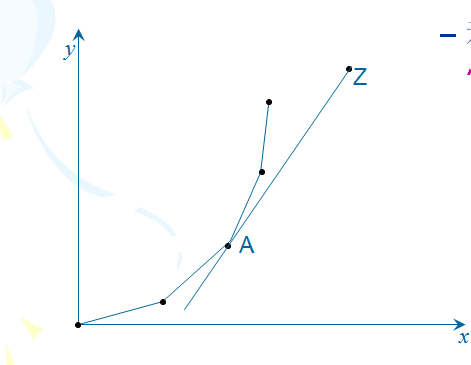
我们就可以看粗A到Z就是最优的，那么我们在每次再队头寻找z的对应最优值A的时候，我们如果找到一个最大的斜率AZ，那么对于在后面的点来说，A前面的点都是没有意义的，也就是说不会也不可能是最优值了，那么我们就可以淘汰掉了，那么最后分摊下来之后复杂度为O(1)。

我们就可以愉快的完美AC了。

但是不要忘记这里还有坑，需要考虑F==N的情况，而且如果两段斜率相等，也是需要淘汰一个的，因为放在那里完全是浪费枚举时间，而且到了后面还会影响后面的更新，所以这些题暴力分很足就先敲暴力，然后敲正解，如果敲不完或者是对拍错了Debug不出来，那么就交暴力程序也是能拿到不错的分数的。

毕竟我还是太弱了QAQ

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<iomanip>
using namespace std;
long long n,a[1000010],m,head=0,tail=0;
long long F,ans=0,Queue[1000010];
inline double Slope(int x,int y)
{ return 1.0*(a[x]-a[y])/(x-y); }
int main()
{
    cin>>n>>F;
    memset(a,0,sizeof(0));
    Queue[0]=0;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
        a[i]+=a[i-1];
    }
    if(n==F)
    {
        cout<<(a[n]*1000/n)<<endl;
        return 0;
    }
    for(int i=F;i<=n;i++)
    {
        while(head<tail&&Slope(i-F,Queue[tail])<=Slope(Queue[tail],Queue[tail-1])) tail--;
        Queue[++tail]=i-F;
        while(head<tail&&Slope(i,Queue[head])<=Slope(i,Queue[head+1])) head++;
        ans=max(ans,(long long)1000.0*(a[i]-a[Queue[head]])/(i-Queue[head]));
    }
    cout<<ans<<endl;
    return 0;
}