堆/优先队列

我觉得堆和优先队列是我现在学习到的最神奇的东西了，比sort还要神奇！

堆和优先队列是比较高级的数据结构，效率很高，O(logn)啊！堪比sort，但是实际上并没有sort快，但是也是很方便的。

然后就是使用的时候麻烦一点，需要输入一些不好记住的东西：

堆的定义

priority_queue<int,vector<int>,greater(less)<int(double)> > ans(name);

然后就是头文件：#include<queue>

堆的使用

然后就可以随心所欲的ans.push(a[i])进队，返回队列是否为空ans.empty()，删除第一个元素ans.pop()，返回元素个数ans.size()，返回优先值最高的东西ans.top()。

这就是堆的一些应用，用堆的排序效率并不是太高，仅仅只是一些特别的题目会用到，然后就是完全二叉树了！

完全二叉树

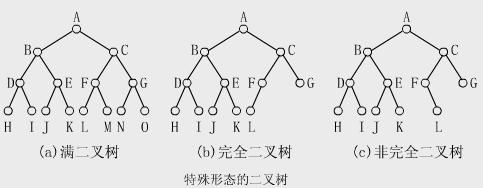
上面的就是二叉树，分别是好用的满二叉树，一边倒的完全二叉树和体型奇异的非完全二叉树。

二叉树直接存储的时候，按照左儿子是自己坐标乘2，右儿子是乘2+1 。

就这样乘就可以用一个结构体，将一个二叉树存储下来！

下面直接看题目：

P1235-FBI树

题目描述：

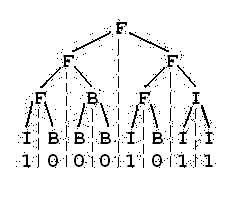
我们可以把由“0”和“1”组成的字符串分为三类：全“0”串称为B串，全“1”串称为I串，既含“0”又含“1”的串则称为F串。 FBI树是一种二叉树[1]，它的结点类型也包括F结点，B结点和I结点三种。由一个长度为2N的“01”串S可以构造出一棵FBI树T，递归的构造方法如下： 1) T的根结点为R，其类型与串S的类型相同； 2) 若串S的长度大于1，将串S从中间分开，分为等长的左右子串S1和S2；由左子串S1构造R的左子树T1，由右子串S2构造R的右子树T2。 现在给定一个长度为2N的“01”串，请用上述构造方法构造出一棵FBI树，并输出它的后序遍历[2]序列。

输入：

第一行是一个整数N（0 ≤ N ≤ 10），第二行是一个长度为2^N的“01”串。

输出：

一行，这一行只包含一个字符串，即FBI树的后序遍历序列。

题解：

这道题，我最开始是用的递归，然后循环比较有多少个0，多少个1什么的，然后发现写来写去，写的我一脸懵逼，写的我想吐。

于是乎，于是乎，我想起来了递推，我想起来了只需要比较左右孩子的F、B、I，的值就好了，一样的话就是和儿子们相同，不一样的话就一定是F，就这样递推过了，一定要记得逆推，先将二叉树的最后一层提前处理完毕，然后两个两个跑，两个比较一下，给爸爸一个明确的值，等到轮到爸爸和叔叔的时候，有会给爷爷一个值，然后不停比较，不停跑就好，一直跑到祖宗节点，一个后序遍历就好！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
#include<string>
using namespace std;
struct FBI
{
    int leftchild;
    int rightchild;
    string s;
};
FBI arr[20000];
void out(int p)
{
    if(p==0) return;
    out(arr[p].leftchild);
    out(arr[p].rightchild);
    cout<<arr[p].s;
    return;
}
int main()
{
    int n,all=0;
    string s1;
    cin>>n>>s1;
    for(int i=s1.size();i>=1;i=i/2)
        all+=i;
    for(int i=all-s1.size()+1;i<=all;i++)
    {
        arr[i].leftchild=0;
        arr[i].rightchild=0;
        if(s1[i+s1.size()-all-1]=='1')
        arr[i].s='I';
        if(s1[i+s1.size()-all-1]=='0')
        arr[i].s='B';
    }
    for(int i=all;i>1;i=i-2)
    {
        if(arr[i].s==arr[i-1].s)
            arr[i/2].s=arr[i].s;
        if(arr[i].s!=arr[i-1].s)
            arr[i/2].s='F';
    }
    for(int i=1;i<=all-s1.size();i++)
        {
            arr[i].leftchild=i*2;
            arr[i].rightchild=i*2+1;
        }
    out(1);
    return 0;
}