Flyed算法

代码：

for(i=1;i<=n;i++)
    for(k=1;k<=n;k++)
 for(j=1;j<=n;j++)
     if(e[i][j]>e[i][k]+e[k][j])
   e[i][j]=e[i][k]+e[k][j];

代码讲解：

这段代码的基本思想就是：最开始只允许经过1号顶点进行中转，接下来只允许经过1和2号顶点进行中转……允许经过1~n号所有顶点进行中转，求任意两点之间的最短路程。用一句话概括就是：从i号顶点到j号顶点只经过前k号点的最短路程。

K循环作用

也就是说，最外层的循环每次枚举的是中间点k，然后下面两个循环不停地枚举通过另外两个点，如果这两个点能够通过k这个点更新掉 i 到 j 的最短路，那么就开始更新，其实我在最开始接触Floyd的时候，有一点很是不理解，那就是为什么k在最外层循环，因为k代表的是 i 和 j 中间的点，为什么k不能在第二层循环或者是第三层循环呢，找了很久的资料之后我才弄明白这个算法中k为什么在最外层，顺便感悟到了这个算法的真正的魅力和神奇。

代码运行

开始算法之前，首先介绍一下这个算法是如何运行的，e[i][j]指的是从 i 到 j 的最短路，在初始化的时候，如果着两条边直接有路相连，那么直接赋值，如果没有连接，那么就设为正无穷大，一般用一个比较大的数。然后每次比较 i 和 j 之间的中间点 k ，如果 i 到k 加上 k 到 j 的权值小于 i 直接到 j 那么 e[i][j]的值也就是 i 到 j 的最短路就变成了从e[i][k]+e[k][j]的值。

K循环最外层证明

但是为什么要先枚举k呢，为什么不能先枚举 i 然后再枚举 i 的中间点k，最后枚举 j 呢，其实这是因为，i=1,j=2时，这时k分别取1,2,…,n，这时1到3，1到4，…..，3到2，4到2，…的距离都不是某种意义上最短的，而这个新算法却直接使用了他们，并且再也没有回头重新计算i到j的距离是否因为其他节点间距离的改变而更短，所以这样算出来的值也就没有什么意义。

K循环最外层证明实例

如果用比较清晰的图来说明的话，如下图：

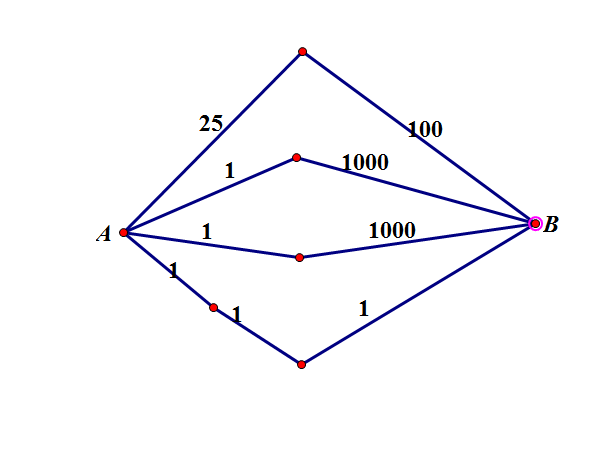
在上面这个图中枚举i=A，j=B，然后循环，正确的A到B最小是3，然而你更新的是125，因为你在枚举下一个i之后，就不会再次回去了，所以说A,B之间的最短路就被定为了125，以后也会以e[i][j]=125去更新其他的点，所以说，k循环必须放在最外层，不然会有可能无法找到最优值。