写在前面：

无良学姐瞎写讲稿，毁我青春，还好有刘神相助，改了错误的地方，不然要栽在书上了……首先说割点，割点的意义在于切掉这个点，就，就不连通了，这个图就毁了，那么这个点就是一个割点，所以说我们在求割点的时候，需要注意一种东西，那就是你搞得图，不一定是联通的，所以你需要遍历所有的联通图……

因为P1230就是这个坑，超级大坑，这个图是不连接的，所以你需要求出所有图的所有割点……

关于割点

割点概念：

在一个无向连通图中，如果有一个顶点集合，删除这个顶点集合以及这个集合中所有顶点相关联的边以后，原图变成多个连通块，就称这个点集为割点集合。

求出割点

然后说如何求出割点，首先我们需要建图，然后开两个数组，一个是dfn，另一个是low，而dfn表示的是DFS的访问时间，low表示的是这个点能回到的最靠前的点。我们建立一个DFS树，按照顺序DFS得到一个树，这个树来说，对于一个树，我们要看他的边，如果这个边是链接下面的点的话，他就是正常边，如果这个边链接上面的点，那么这就不是一个正常的边，我们称作为返祖边，对于返祖边我无话可说，一旦遇到这种返祖边，也就意味着这个返祖边（u，v），dfn[v]<dfn[u] 我们就开始记录下除了父亲之外的所有点能访问到的最小dfn的值，所以说对于x的一个儿子y，如果low[y]>=dfn[x] 那么就说明y中不存在想x的祖先的返祖边，并且这种访问是不可以访问父亲的……

比如下面这张图片：

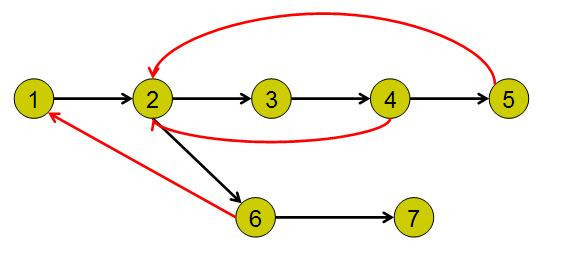
ps：红边为返祖边……

然后直接DFS，每次枚举x到y的边。

1.如果y是x的父亲，就跳过（因为我们不访问父亲点）

2.如果y被访问，那么就是返祖边（因为之前已经访问到了，只能返祖边再次对他访问）

3.如果y没有被访问的话，就对y进行DFS，用low[y]来更新low[x]，并判断low[y]是否大于等于dfn[x]，如果是，那么字树+1。

注意，代码中实现是递归实现的，所以遍历到所有的点之后，然后逐次返回到上一个值，然后进行处理，所以说在判断这个子树有没有返祖边的时候，比较low[y]和dfn[x]是成立的。

最后来求出割点，如果为根节点，那么字树需要大于等于2，如果不是根节点，只需要大于等于1就可以了。

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
void tarjan(int x,int par=0)
{
	dfn[x]=low[x]=++ind;
	int son=0;
	for(int i=Line[x],y;i;i=a[i].next)
	if((y=a[i].point)!=par)
	{
		if(!dfn[y])
		{
			tarjan(y,x);
			if(low[y]<low[x])
			low[x]=low[y];
			if(low[y]>=dfn[x])
			son++;
		}
		else if(dfn[y]<low[x])
		low[x]=dfn[y];
	}
	if(son>=2||(son==1&&par))
	ans[++tot]=x;
}

割点判断

然后呢，就是可爱的割边了！

说道割边，那么我们试问，割边的两个点是不是割点呢，两个割点所连接的边是否为割边？？？

然而都不是，都不是，具体原因可以参看下面的图片……

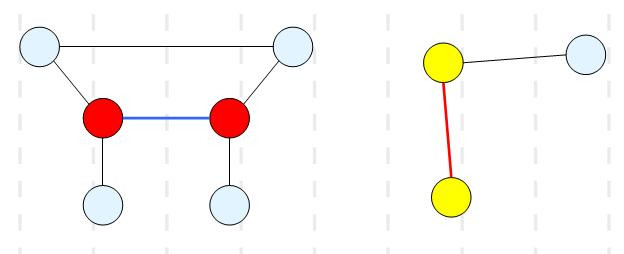
关于割边

割边概念：

假设有连通图G，e是其中一条边，如果G-e是不连通的，则边e是图G的一条割边。

割边判断：

有了割点作为基础，我们就可以搞割边了，首先返祖边绝对不会是割边的，因为去掉了返祖边对整个图是没有什么影响的，所以说我们找到没有返祖边，也就是说，如果不去访问父节点，那么无法到比自己还要靠前的边，这个就是一个割边……

和割点一样，我们不断更新他的dfn和low的值，然后最后进行比较，值得一提的是你需要提前来建立一个数组，暂且叫他rev，其中rev[i]表示的是 i 这个编号中，他的反向边的编号，这个是用来判断下一次访问是否是父节点，如果反向边的编号等于了下次访问的边的编号，那么就GG了，这是访问父节点……

然后我们判断割边的条件就是，如果这个点不是根节点，并且这个点在不访问父节点的情况下，最前面能到达的点就是自己的话，那么它到它父亲这条边就是一个割边。

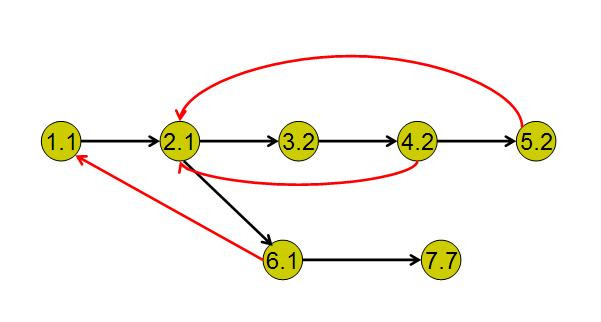
上面的图要配合着第一张图来看，其中点后面的数字表示最早访问点……

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
void Cut_Edge(int x,int par=0)
{
    dfn[x]=low[x]=++ind;
    for(int i=Line[x];i!=0;i=a[i].next)
    if(i!=par)
    {
        int y=a[i].y;
        if(!dfn[y])
        {
            Cut_Edge(y,rev[i]);//rev代表的是其反向边；
            low[x]=min(low[x],low[y]);
        }
        else low[x]=min(low[x],dfn[y]);
    }
    if(dfn[x]==low[x]&&par!=0)
    {
        ans[++top].x=min(a[par].x,a[par].y);
        ans[top].y=max(a[par].x,a[par].y);
    }
}

关于强连通分量

强连通分量：

有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。

强连通分量求法：

然后就是强联通分量……

说到强连通分量这种东西啊，真的是非常神奇呢，

首先说一下强连通分量的定义啊，强连通分量集合中，每两个元素之间，都有一条有向边可以互相到达的集合叫做强连通分量集合，比如下图：

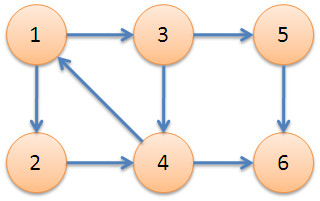
这张图片中，所有的强连通分量有：{1,2,3,4}，{5}，{6}；这三个，比如第一个集合中，1到4可以通过3来到达，3到1有一条直接相连的边，这样就保证了在集合{1,2,3,4}中，每个元素之间，都有一条有向边可以互相到达……

在求强连通分量的时候，我们需要用到一个叫做栈的东西，和以往一样的，我们需要建立一个dfn和low两个值，然后不停地在DFS过程中记录下来最早值和访问时间，如果没有被访问，那么就去访问他，然后压到栈里面，如果没有被访问，就更新low的值，并且判断dfn是否等于low，如果相等，那么这个x在弹栈前面（包括自己）所有的点都能构成一个联通分量。

至于为什么，因为在这个栈里面，自己前面所有的点都是自己遍历过的，那么如果自己前面的点都能够回到自己这里，那么当到达这个x点的时候，如果x不能回到之前的点，那么这个联通分量最大也就是这么大了，因为这是联通的极限了，所有如果low==dfn的话，表明自己不能在往前走了，而自己后面的点都是和自己联通的，那么，自己就是这个连通分量的最终地方，也就是说，在这个栈里面，自己之前的所有点包括自己都是一个连通分量，当且仅当low[u]==dfn[u]时，u以及在u之后被加入栈的点构成一个强连通分量，而这些点将会在u的DFS结束时被从栈中弹出。

1.若y未被访问过，递归访问y之后用low[y]更新low[x]。

2.若y被访问过且y在栈中，那么用dfn[y]更新low[x]。

3.在递归结束如果dfn[x]==low[x]，将x及之后的点弹出栈，标记它们属于同一个强连通分量。

上面就是找联通分量的一个过程了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
void tarjan(int x)
{
    dfn[x]=low[x]=++ind;
    stack[++top]=x;
    ins[x]=true;
    for(int i=Line[x];i!=0;i=a[i].next)
    {
        int y=a[i].y;
        if(!dfn[y])
        {
            tarjan(y);
            low[x]=min(low[x],low[y]);
        }else if(ins[y]==true)
        low[x]=min(low[x],dfn[y]);
    }
    if(dfn[x]==low[x])
    {
        int k,The_tall=0;
        tot++;
        do
        {
            The_tall++;
            k=stack[top--];
            ins[k]=false;
            bel[tot]++;
            ans[tot][bel[tot]]=k;
        }while(k!=x);
    }
}

割边，割点和强连通分量就告一段落了，真是搞了好久……是时候看DP了！