单调队列描述
于队列,就是一个数组,不过需要用head(我习惯用top)和tail(我习惯用end)来维护的一个先进后出的队列(有时候出入不规则)。单调队列就是在整个队列中,所有元素都是单调递增或者单调递减的,因为需要维护整个队列为单调的,所以有时候需要在队头或者队尾都删除数。
单调队列和单调栈是相似的,但是最优解的范围不同,队列在乎全局P1157,栈在乎局部P1153.
题目P1157window
题目描述:
给你一个长度为 N 的数组,一个长为 K 的滑动的窗体从最左移至最右端, 你只能见到窗口的K个数,每次窗体向右移动一位,如下表:
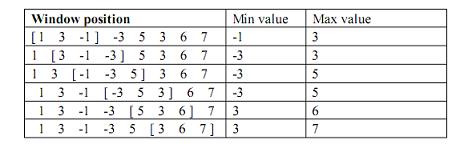
你的任务是找出窗口在各位置时的 max value,min value.
输入:
-第 1 行 n,k,
-第 2 行为长度为 n 的数组;
输出:
2 行 第 1 行每个位置的 min value,
第 2 行每个位置的 max value ;
题解:
拿到这道题,最简单的方法,n-k个sort,也就是说(n-k)*nlogn 次计算,如果n大一点,绝对超时,那么为了有更快的办法,我们可以直接使用单调队列来解决这个问题。因为题目中有min和max所以就需要两个不同的单调队列了,一个来存储递增的,另一个是递减的。
我们可以首先算出窗户最开始时的队列:
1
2
3
4
5
6
7
| for(int i=2;i<k;i++)
{
while(a[i]<e[end].v&&end>=top)
end--;
e[++end].sit=i;
e[end].v=a[i];
}
|
这样利用while(a[i]<e[end].v&&end>=top)来比较元素,然后保证新进入的元素都是单调的,这样重复就好,然后再从k到n进行一次,和上面一样,不过需要多一个判断,判断top对头的元素有没有出去window的范围,如果出去了,就需要删除掉他。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
| #include<iostream>
#include<algorithm>
using namespace std;
struct note//结构体,用来存储队列里面的位置和权值
{
long long v;
long long sit;
};
note e[1000001],q[1000001];
long long a[1000001];
int main()
{
long long n,k;
cin>>n>>k;
long long top=1,end=1;
for(int i=1;i<=n;i++)
cin>>a[i];
e[1].v=a[1];
e[1].sit=1;
for(int i=2;i<k;i++)
{
while(a[i]<e[end].v&&end>=top)
end--;
e[++end].sit=i;
e[end].v=a[i];
}
for(int i=k;i<=n;i++)
{
if(i-e[top].sit==k) top++;
while(a[i]<e[end].v&&end>=top)
end--;
e[++end].v=a[i];
e[end].sit=i;
cout<<e[top].v<<' ';
}
cout<<endl;
end=1;
top=1;
q[1].v=a[1];
q[1].sit=1;
for(int i=2;i<k;i++)
{
while(a[i]>q[end].v&&end>=top)
end--;
q[++end].sit=i;
q[end].v=a[i];
}
for(int i=k;i<=n;i++)
{
if(i-q[top].sit==k) top++;
while(a[i]>q[end].v&&end>=top)
end--;
q[++end].v=a[i];
q[end].sit=i;
cout<<q[top].v<<' ';
}
return 0;
}
|
